4021. Knight move
The rectangular board of size n × m (n rows and m columns) is given. The chess knight is
located in the left upper corner. You must relocate it to the right lower
corner. The knight can move only either two cells down and one right, or one
cell down and two cells right.
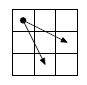
Find the number of knight paths from
the left upper corner to the right lower corner.
Input. Two
positive integers n and m (1 ≤ n, m ≤ 50).
Output. Print
the number of ways to relocate the knight from the left upper corner to the
right lower corner of the board.
|
Sample input 1 |
Sample output 1 |
|
3 2 |
1 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
31 34 |
293930 |
SOLUTION
dynamic programming
Algorithm
analysis
Let dp[i][j] contains the number
of ways to run from left upper corner – the cell with coordinates (1, 1) into
right lower corner – the cell with coordinates (n, m). Assign zeroes to
array dp and set dp[1][1] = 1.
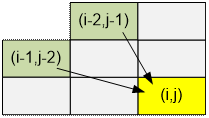
According to the knight moves, we can
come into cell (i, j) only either from (i – 1, j – 2) or from (i – 2, j – 1). So
dp[i][j] = dp[i – 1][j – 2] + dp[i – 2][j – 1]
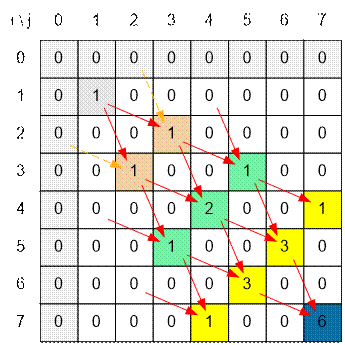
Sample
Fill the array dp for the board of
size 7 * 7:
Algorithm
realization
Declare two dimensional array.
#define MAX 55
int dp[MAX][MAX];
Read
the input data.
scanf("%d
%d",&n,&m);
Calculate
the values for elements of array dp. Since
the knight can not get into the cells of the first row and the first column (except
the initial position), then the loops by i and
by j can be started from 2.
memset(dp,0,sizeof(dp));
dp[1][1] = 1;
for (i = 2; i <= n; i++)
for (j = 2; j <= m; j++)
dp[i][j] = dp[i-1][j-2] + dp[i-2][j-1];
Print the answer.
printf("%d\n",dp[n][m]);
Java
realization
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
long dp[][] = new long [n+1][m+1];
dp[1][1] = 1;
for (int i = 2; i <= n; i++)
for (int j = 2; j <= m;j ++)
dp[i][j] = dp[i-1][j-2] + dp[i-2][j-1];
System.out.println(dp[n][m]);
con.close();
}
}