4033. Трамвай
Трамвайная сеть
в Загребе состоит из множества перекрестков и рельсов, соединяющих их. На
каждом перекрестке имеется переключатель, указывающий на один из рельсов,
выходящих из него. Когда трамвай въезжает на перекресток, он может покинуть его
только в том направлении, на которое указывает переключатель. Если водитель
хочет идти другим путем, он должен вручную изменить переключатель.
Когда водитель
едет от перекрестка a к перекрестку b, он старается выбрать путь, на котором
количество изменений состояний переключателей минимально.
Напишите
программу, которая вычислит наименьшее число изменений переключателей,
необходимых для проезда от пересечения a
до пересечения b.
Вход. Первая строка содержит целые числа n, a и b (2 ≤ n ≤ 105, 1 ≤ a, b ≤ n), где n – количество
перекрестков в сети, перекрестки пронумерованы числами от 1 до n.
Каждая из
следующих n строк содержит
последовательность чисел, разделенных пробелом. Первое число в i-ой строке ki (0 ≤ ki
≤ n – 1), указывающее на
количество трамвайных путей, исходящих из i-го
перекрестка. Следующие ki
чисел указывают номера перекрестков, непосредственно связанными с i-ым. Переключатель на i-ом перекрестке изначально указывает на
перекресток, который первым указан в списке смежности.
Выход. Выведите наименьшее искомое количество переключений. Если
проехать от a до b невозможно, то выведите -1.
|
Пример
входа |
Пример
выхода |
|
3 2 1 2 2 3 2 3 1 2 1 2 |
0 |
РЕШЕНИЕ
графы -
поиск в ширину
Анализ алгоритма
Построим граф, в
котором вершинами будут перекрестки, а ребрами – всевозможные трамвайные пути.
Если на перекрестке x переключатель
стоит по направлению к перекрестку y,
то положим вес ребра (x, y) равным 0. Если от x можно изменить состояние переключателя
к y, то вес ребра (x, y)
положим равным 1.
Таким образом при
движении от перекрестка a к
перекрестку b мы будем минимизировать
не длину пути, а количество переключений. Получили 0-1 граф. Алгоритм Дейкстры
даст Time Limit. Воспользуемся поиском в ширину с релаксацией ребер:
·
если релаксирует ребро (x, y) весом 1, то кладем y в конец очереди.
·
если релаксирует ребро (x, y) весом 0, то кладем y в начало очереди.
Пример
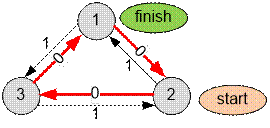
Ребра с весом 0
указывают на начальное состояние направлений переключателей.
Реализация алгоритма
Входной взвешенный
граф храним в списке смежности g. Объявим
массив кратчайших расстояний dist.
Объявим константу бесконечность INF.
#define INF 0x3F3F3F3F
vector<int> dist;
vector<vector<pair<int, int> >
> g;
Функция bfs реализует поиск в ширину из вершины start. Положим кратчайшее расстояние от стартовой вершины до всех
остальных равными INF. Расстояние от start
до start равно 0.
void bfs(int
start)
{
dist = vector<int>(n+1,INF);
dist[start] = 0;
deque<int>
q;
q.push_back(start);
while(!q.empty())
{
int v =
q.front(); q.pop_front();
for(int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i].first;
int w =
g[v][i].second;
Если ребро (v, to) релаксирует, то пересчитываем
кратчайшее расстояние dist[to].
if
(dist[to] > dist[v] + w)
{
dist[to] = dist[v] + w;
В зависимости от веса релаксируемого ребра заносим вершину to в конец или в начало очереди.
if (w
== 1)
q.push_back(to);
else
q.push_front(to);
}
}
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d",&n,&a,&b);
g.resize(n+1);
for(i = 1; i <= n; i++)
{
Читаем количество ребер k, исходящих из
вершины i.
scanf("%d",&k);
for(j = 0; j
< k; j++)
{
scanf("%d",&to);
В i-ой строке после
числа ki стоит номер
перекрестка, на который указывает переключатель. Вес этого ребра равен 0. Веса
всех остальных исходящих ребер равны 1.
w = (j == 0) ? 0 : 1;
g[i].push_back(make_pair(to,w));
}
}
Запускаем поиск в ширину из вершины а.
bfs(a);
Выводим ответ.
if (dist[b] == INF)
printf("-1\n");
else
printf("%d\n",dist[b]);