4033. Tram
Tram network in
Zagreb consists of several intersections and rails connecting some of them. In
every intersection there is a switch pointing to the one of the rails going out
of the intersection. When the tram enters the intersection it can leave only in
the direction the switch is pointing. If the driver wants to go some other way,
he/she must manually change the switch.
When a driver has
do drive from intersection a to the
intersection b he/she tries to choose
the route that will minimize the number of times he/she will have to change the
switches manually.
Write a program
that will calculate the minimal number of switch changes necessary to travel
from intersection a to intersection b.
Input. The first line contains integers n, a
and b (2 ≤ n ≤ 105, 1 ≤ a, b ≤ n), where n is the
number of intersections in the network, numbered from 1 to n.
Each of the
following n lines contain a sequence
of integers separated by a single blank character. First number in the i-th line, ki (0 ≤ ki
≤ n – 1), represents the number
of rails going out of the i-th
intersection. Next ki numbers
represents the intersections directly connected to the i-th intersection. Switch in the i-th intersection is initially pointing in the direction of the
first intersection listed.
Output. The only line should contain the target
minimal number. If there is no route from a
to b the line should contain the
integer -1.
|
Sample
input |
Sample
output |
|
3 2 1 2 2 3 2 3 1 2 1 2 |
0 |
SOLUTION
graphs, breadth first
search, 0-1 graph
Algorithm analysis
Construct a graph
in which the vertices are the crossroads, and the edges are all kinds of tram
lines. If the switch at the intersection x
is in the direction of the intersection y,
then set the weight of the edge (x, y) to 0. If we can change the state of
the switch from x to y, then the weight of the edge (x, y)
set to 1.
Thus, when
moving from intersection a to
intersection b, we’ll minimize not
the path length, but the number of switches. We have a 0 – 1 graph. Dijkstra’s algorithm gives Time Limit. Use breadth first search with edge relaxation:
·
if an edge (x, y) of weight 1 relaxes, then push y to the end of the queue;
·
if an edge (x, y) of weight 0 relaxes, then push y to the front of the queue;
Example
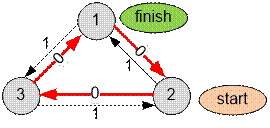
The edges with
weight 0 indicate the initial state of the switch directions.
Algorithm realization
Store the input
weighted graph in the adjacency list g.
Declare an array
of shortest distances dist. Declare a
constant infinity INF.
#define INF 0x3F3F3F3F
vector<int> dist;
vector<vector<pair<int, int> >
> g;
Function bfs implements the breadth first search from the vertex start. Set the shortest
distance from the starting vertex to all the others equal to INF. The distance
from start to start set to 0.
void bfs(int
start)
{
dist = vector<int>(n+1,INF);
dist[start] = 0;
deque<int>
q;
q.push_back(start);
while(!q.empty())
{
int v =
q.front(); q.pop_front();
for(int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i].first;
int w =
g[v][i].second;
If the edge (v, to) relaxes, then recompute the shortest
distance dist[to].
if
(dist[to] > dist[v] + w)
{
dist[to] = dist[v] + w;
Depending on the weight of the relaxed edge, push the vertex to either at the end or at the start of the queue.
if (w
== 1)
q.push_back(to);
else
q.push_front(to);
}
}
}
}
The main part of the program. Read the input data.
scanf("%d %d %d",&n,&a,&b);
g.resize(n+1);
for(i = 1; i <= n; i++)
{
Read the number k of edges
outgoing from vertex i.
scanf("%d",&k);
for(j = 0; j
< k; j++)
{
scanf("%d",&to);
In the i-th line,
after the number ki, there is a number of intersection where the switch
points to. The weight of
this edge is 0. The weight of all other outgoing edges is 1.
w = (j == 0) ? 0 : 1;
g[i].push_back(make_pair(to,w));
}
}
Start the breadth first search from the vertex a.
bfs(a);
Print the answer.
if (dist[b] == INF)
printf("-1\n");
else
printf("%d\n",dist[b]);