4051. Кузнечик

У одного из преподавателей в комнате живёт кузнечик, который очень любит прыгать по одномерной клетчатой доске. Длина доски n клеток. К его сожалению, он умеет прыгать только на 1, 2, ..., k клеток вперёд.

Однажды преподавателям стало интересно, сколькими способами кузнечик может допрыгать из первой клетки до последней. Помогите им ответить на этот вопрос.

Вход. Два целых числа n и k (1 ≤ n ≤ 30, 1 ≤ k ≤ 10).

Выход. Выведите количество способов, которыми кузнечик может допрыгать из первой клетки до последней.

Пример входа	Пример выхода
8 2	21

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть dp[i] равно количеству способов, которыми кузнечик сможет допрыгать из первой до i-ой клетки. Положим dp[1] = 1, dp[2] = 1.

Если 2 < i ≤ k, то попасть в i-ую клетку можно из любой предыдущей, так что

dp[i] = dp[1] + dp[2] + … + dp[i – 1] =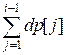

Пусть k велико, подсчитаем dp[i] по этой формуле:

dp[3] = dp[1] + dp[2] = 1 + 1 = 2,

dp[4] = dp[1] + dp[2] + dp[3] = 1 + 1 + 2 = 4,

dp[5] = dp[1] + dp[2] + dp[3] + dp[4] = 1 + 1 + 2 + 4 = 8

Можно заметить, что dp[i] = 2* dp[i – 1]. Однако эту формулу можно получить из следующих соображений. Из того что

dp[i – 1] = dp[1] + dp[2] + … + dp[i – 2]

следует что

dp[i] = (dp[1] + dp[2] + … + dp[i – 2]) + dp[i – 1] =

dp[i – 1] + dp[i – 1] = 2 * dp[i – 1]

Если i > k, то попасть в i-ую клетку можно из любой из k предыдущих, так что

dp[i] = 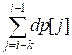= dp[i – k] + … + dp[i – 1]

Аналогично можно заметить, что из того что

dp[i – 1] = dp[i – k – 1] + … + dp[i – 2]

следует что

dp[i] = dp[i – k] + … + dp[i – 1] =

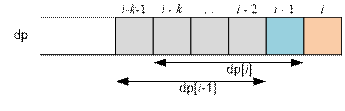
(dp[i – k – 1] + dp[i – k] + … + dp[i – 2]) – dp[i – k – 1] + dp[i – 1] =

2 * dp[i – 1] – dp[i – k – 1]

Пример

Для приведенного в примере теста n = 8 и k = 2 состояние массива dp имеет вид:

Если n = 8 и k = 4, то массив dp примет вид:

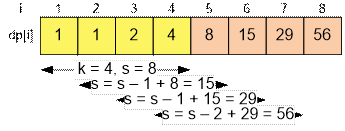
Упражнение

Заполните массив dp для n = 8 и k = 3.

Реализация алгоритма

Объявим рабочий массив.

#define MAX 35

int dp[MAX];

Читаем входные данные. Инициализируем dp[1] = dp[2] = 1.

scanf("%d %d",&n,&k);

dp[1] = 1; dp[2] = 1;

Заполняем ячейки массива dp[i] для 2 < i ≤ k.

for(i = 3; i <= k; i++)

dp[i] = 2 * dp[i-1];

Заполняем ячейки массива dp[i] для i > k.

for(; i <= n; i++)

dp[i] = 2 * dp[i-1] - dp[i-k-1];

Выводим ответ.

printf("%d\n",dp[n]);

Java реализация

import java.util.*;

class Main

{

static int dp[] = new int[35];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int k = con.nextInt();

int i;

dp[1] = 1; dp[2] = 1;

for(i = 3; i <= k; i++)

dp[i] = 2 * dp[i-1];

for(; i <= n; i++)

dp[i] = 2 * dp[i-1] - dp[i-k-1];

System.out.println(dp[n]);

con.close();

}

}

Python реализация

Объявим константу MAX.

MAX = 35

Читаем входные данные.

n, k = map(int, input().split())

Инициализируем ячейки списка dp.

dp = [0] * MAX

dp[1] = 1

dp[2] = 1

Заполняем ячейки массива dp[i] для 2 < i ≤ k.

for i in range(3, k + 1):

dp[i] = 2 * dp[i - 1]

Заполняем ячейки массива dp[i] для i > k.

for i in range(max(3, k + 1), n + 1):

dp[i] = 2 * dp[i - 1] - dp[i - k - 1]

Выводим ответ.

print(dp[n])