4076. Генератор простых чисел

 

Петр хочет сгенерировать несколько простых чисел для своей криптосистемы. Помогите ему! Вам следует сгенерировать все простые числа между двумя заданными.

 

Вход.  В первой строке содержится количество тестов t (t ≤ 10). В каждой из следующих t строк содержится два числа m и n (1 ≤ m ≤ n ≤ 109, n – m ≤ 105), разделенных одним пробелом.

 

Выход. Для каждого теста вывести все простые числа p, удовлетворяющие m ≤ p ≤ n, по одному числу в строке. Тесты следует разделять пустой строкой.

 

Пример входа

Пример выхода

2

1 10

3 5

2

3

5

7

 

3

5

 

 

РЕШЕНИЕ

решето Эратосфена

 

Анализ алгоритма

В задаче необходимо реализовать решето Эратосфена на отрезке. Информацию о простоте чисел [m … n] будем хранить в primes[0 ... n – m]. Перебираем все возможные делители p = 2, 3, 5, 7, …,  чисел на отрезке и отмечаем в массиве primes кратные им как составные.

Пусть low – наименьшее число из отрезка [m … n], кратное p. Тогда все числа j = low + pk (k = 0, 1, 2, …), не большие n, следует установить составными (primes[j – m] = 0) так как все они делятся на p. При этом если j = p, и p простое то primes[j – m] следует оставить равным 1 (число j простое).

 

Пример

Промоделируем работу решета на отрезке [3; 12]. Изначально все числа объявим простыми. Поскольку  = 3, то достаточно перебрать делители 2 и 3.

 

p = 2: все числа, кратные 2, объявляем составными. Числа 2 в массиве нет.

 

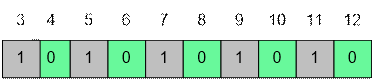
p = 3: все числа, кратные 3, объявляем составными. Число 3 в массиве есть, поэтому его оставляем простым.

 

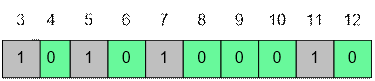
Реализация алгоритма

В массиве primes будем отмечать простоту чисел от m до n: ячейка содержит 1, если число простое и 0 иначе. При этом ячейка primes[0] содержит информацию о простоте числа m.

 

int primes[100010];

 

Читаем входные данные.

 

scanf("%d",&tests);

while(tests--)

{

  scanf("%d %d",&m,&n);

 

Изначально все числа на отрезке [m .. n] пусть будут простыми.

 

  for(i = 0; i < n - m + 1; i++) primes[i] = 1;

 

Перебираем все возможные делители p чисел с отрезка: стартуем с двойки, а потом перебираем все нечетные числа, начиная с 3 и вплоть до .

 

  for(p = 2; p <= (int)sqrt(1.0*n); p += 2)

  {

 

   Пусть наименьшее число, которое делится на p и не меньше m, равно low.

 

    low = m / p * p;

    if (low < m) low += p;

 

Проходим циклом по j от low до n с шагом p. Все пройденные числа j будут делиться на p, поэтому в массиве primes отмечаем их как составные (primes[j – m] = 0). При этом:

·        Если j = p простое, то primes[p – m] следует оставить равным 1.

·        Если j = p – нечетное составное, которое принадлежит отрезку [m .. n], то primes[p – m] установлено в 0 было ранее, когда рассматривался простой делитель числа p.

 

    for(j = low; j <= n; j += p)

      if (j != p) primes[j - m] = 0;

 

Изначально p равнялось 2. Далее в цикле p будет принимать значения нечетных чисел: 3, 5, 7, . . . .

 

    if (p == 2) p--;

  }

 

Выводим простые числа на отрезке [m .. n]. Число 1 не является простым.

 

  for(i = m; i <= n; i++)

    if ((primes[i - m] == 1) && (i != 1)) printf("%d\n",i);

 

Тесты между собой разделяем пустой строкой.

 

  if (tests) printf("\n");

}