4077. Corporation salary
You are working in the HR
department of a huge corporation. Each employee may have several direct
managers and/or several direct subordinates. Of course, his subordinates may
also have their own subordinates, and his direct managers may have their own managers.
We say employee x is a boss of
employee y if there exists a sequence
of employees a, b, …, d, such that x is the manager of a, a is the
manager of b, and so on, and d is the manager of y (of course, if x is a
direct manager of employee y, x will be a boss of employee y). If
a is a boss of b, then b can not be a
boss of a. According to the new
company policy, the salary of an employee with no subordinates is 1. If an
employee has any subordinates, then his salary is equal to the sum of the salaries
of his direct subordinates.
You will be given the
relations among employees. Find the sum of the salaries of all the employees.
Input. Contains multiple test
cases. The first line of each test case contains the number of employees n (n
≤ 50). In the next n lines you
are given the relations, where the j-th
character of the i-th element is ‘Y’
if employee i is a direct manager of
employee j, and ‘N’ otherwise.
Output. For each test case print in
a separate line the sum of the salaries of all the employees.
|
Sample input |
Sample output |
|
1 N 4 NNYN NNYN NNNN NYYN 6 NNNNNN YNYNNY YNNNNY NNNNNN YNYNNN YNNYNN |
1 5 17 |
SOLUTION
graph – depth first search
Algorithm analysis
Run the depth first search on
a directed graph, given by adjacency matrix. Function dfs(i) computes the salary of
the i-th employee and
stores it in salary[i]. The sum of the salaries of all
employees is equal to the sum of array elements salary.
Example
The graphs given
in the second and the third
tests are shown below. Near each vertex the employee’s salary is given. The edges of the dfs tree are shown
in red.
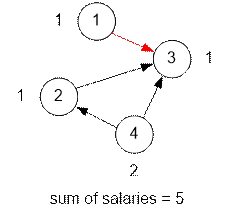
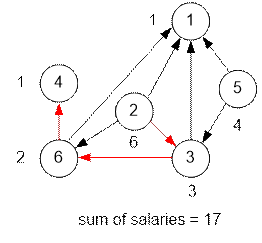
Algorithm realization
Store the
adjacency matrix of the graph in the array rel. Compute the
salary of the i-th employee in salary[i].
#define MAX 51
long long salary[50];
char
rel[MAX][MAX];
Function dfs performs a depth first search from vertex i
and
computes the salary of the i-th employee.
long long dfs(int i)
{
int j;
long long &res = salary[i];
If the salary of the i-th employee is already computed (salary[i] ≠
0), then terminate the search.
if (salary[i]
> 0) return salary[i];
Otherwise start the depth first search from all sons of the vertex i, and compute the salaries of all subordinates of the i-th employee. The salary of the i-th employee is equal to the sum of the salaries of all his
subordinates.
for(res = j =
0; j < n; j++)
if
(rel[i][j] == 'Y') res += dfs(j);
If res = 0, then i-th employee has no subordinates. Set its salary equal to 1.
if (res == 0)
res = 1;
return res;
}
The main part of the program. Read the adjacency matrix of the graph into array rel.
while(scanf("%d\n",&n) == 1)
{
for(i = 0; i
< n; i++) gets(rel[i]);
memset(salary,0,sizeof(salary));
Start the depth first search on a directed graph. Find the salary of each employee.
for(i = 0; i
< n; i++)
if
(!salary[i]) dfs(i);
Find and
print the total salary of all employees res.
for(res = i =
0; i < n; i++)
res += salary[i];
printf("%lld\n",res);
}
Java realization
import java.util.*;
import java.io.*;
public class Main
{
static String rel[];
static long salary[];
public static long dfs(int i)
{
int j;
if (salary[i] > 0) return salary[i];
for(j = 0; j < rel.length; j++)
if (rel[i].charAt(j) == 'Y') salary[i] += dfs(j);
if (salary[i] == 0) salary[i] = 1;
return salary[i];
}
public static void main(String[] args) throws IOException
{
//Scanner con = new Scanner(new
FileReader ("4077.in"));
Scanner con = new Scanner(System.in);
while(con.hasNext())
{
int n = con.nextInt();
rel = new String[n];
for(int i = 0; i < n; i++)
rel[i] = con.next();
long res = 0;
salary = new long[n];
for(int i = 0; i < n; i++)
if (salary[i] == 0) dfs(i);
for(int i = 0; i < n; i++)
res += salary[i];
System.out.println(res);
}
con.close();
}
}