4104. Расстояние в дереве

Связный граф, не содержащий циклов, называется деревом.

Расстоянием между двумя вершинами дерева называется длина (в рёбрах) кратчайшего пути между ними.

Дано дерево из n вершин и натуральное число k. Посчитайте количество различных пар вершин дерева, расстояние между которыми равно k. Обратите внимание, что пары (v, u) и (u, v) считаются одной и той же парой.

Вход. В первой строке записаны два целых числа n и k (1 ≤ n ≤ 50000, 1 ≤ k ≤ 500) – количество вершин дерева и требуемое расстояние между вершинами.

В следующих n – 1 строках описаны рёбра дерева в формате a_i b_i (1 ≤ a_i, b_i ≤ n, a_i ≠ b_i), где a_i и b_i – вершины, соединенные i-ым ребром. Все ребра различны.

Выход. Выведите  одно целое число – количество различных пар вершин дерева, расстояние между которыми равно k.

Пример входа	Пример выхода
5 2 1 2 2 3 3 4 2 5	4

РЕШЕНИЕ

динамическое программирование на дереве

Анализ алгоритма

Пусть dp[v][x] – количество вершин, находящихся на расстоянии x от вершины v в поддереве с корнем в v. Положим dp[v][0] = 1, так как на расстоянии 0 от вершины v находится только сама вершина v.

Пусть вершина v имеет сыновей u₁, u₂, .., u_p. Тогда количество вершин, находящихся на расстоянии x от вершины v в поддереве с корнем в v, равно сумме количеств вершин, находящихся на расстоянии x – 1 от каждой из вершин u₁, u₂, .., u_p.

dp[v][x] =

Рассмотрим поддерево с корнем в вершине v. Подсчитаем количество путей длины k, полностью лежащих в этом поддереве и проходящих через вершину v. Разобьём такие пути на две группы:

· пути, начинающиеся в вершине v. Их количество равно dp[v][k].

· пути, проходящие через вершину v, концы которых расположены в поддеревьях сыновей вершины v.

Рассмотрим путь длины k, проходящий через корень поддерева v. Пусть расстояние от вершины v до одного из концов пути равно x (1 ≤ x ≤ k – 1). Предположим, что этот конец находится в поддереве некоторого сына u₁. Тогда расстояние от вершины v до второго конца пути равно k – x, причём второй конец может находиться в любом другом поддереве, отличном от поддерева с корнем в u₁.

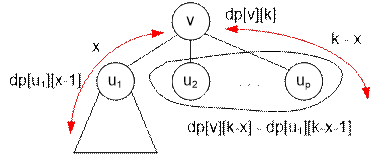
Если расстояние от первого конца пути до вершины v равно x, то расстояние от этого конца до вершины u₁ равно x – 1. Число способов выбрать такой первый конец равно dp[u₁][x – 1].

Число способов выбрать второй конец пути равно количеству вершин, находящихся на расстоянии k – x от вершины v, но не принадлежащих поддереву с корнем в u₁. Это количество равно

dp[v][k – x] – dp[u₁][k – x – 1]

Согласно правилу произведения, общее количество таких путей равно

dp[u₁][x – 1] * (dp[v][k – x] – dp[u₁][k – x – 1])

Таким образом, общее количество таких путей равно

dp[v][k] +

Остается просуммировать указанное выражение по всем вершинам дерева.

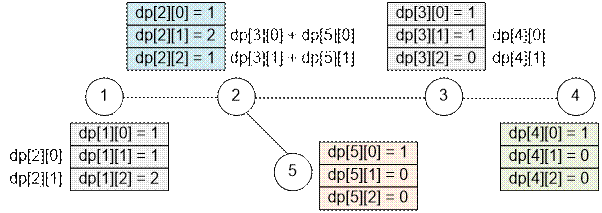
Пример

Рассмотрим дерево, приведенное в примере.

Реализация алгоритма

В массиве g хранится представление дерева в виде списков смежности. Массив dp используется для реализации динамического программирования.

vector<vector<int> > g;

vector<vector<int> > dp;

Функция dfs выполняет поиск в глубину, начиная с вершины v. Значение p обозначает предка вершины v. В процессе обхода строим массив dp.

void dfs(int v, int p = -1)

{

Инициализируем массив dp[v].

dp[v].resize(k+1);

dp[v][0] = 1;

Перебираем все вершины to, в которые можно перейти из вершины v.

for (int to : g[v])

{

if (to == p) continue;

dfs(to,v);

for(int x = 1; x <= k; x++)

dp[v][x] += dp[to][x-1];

}

}

Функция dfsRes выполняет поиск в глубину, начиная с вершины v, и предназначена для вычисления искомого ответа.

void dfsRes(int v, int p = -1)

{

for (int to : g[v])

{

if (to == p) continue;

dfsRes(to,v);

for(int x = 1; x < k; x++)

resA += 1LL * dp[to][x-1] * (dp[v][k-x] - dp[to][k-x-1]);

}

resB += dp[v][k];

}

Основная часть программы. Читаем входные данные. Строим дерево.

scanf("%d %d",&n,&k);

g.resize(n+1);

for (i = 0; i < n - 1; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

g[b].push_back(a);

}

Первым поиском в глубину строим массив dp.

dp.resize(n+1);

dfs(1);

Подсчитываем и выводим искомый ответ.

resA = resB = 0;

dfsRes(1);

res = resA / 2 + resB;

printf("%lld\n",res);

Python реализация

Функция dfs выполняет поиск в глубину, начиная с вершины v. Значение p обозначает предка вершины v. В процессе обхода строим массив dp.

def dfs(v, p):

Инициализируем массив dp[v].

dp[v] = [0] * (k + 1)

dp[v][0] = 1

Перебираем все вершины to, в которые можно перейти из вершины v.

for to in g[v]:

if to == p: continue

dfs(to, v)

for x in range(1, k + 1):

dp[v][x] += dp[to][x - 1]

Функция dfsRes выполняет поиск в глубину, начиная с вершины v, и предназначена для вычисления искомого ответа.

def dfsRes(v, p):

global resA, resB

for to in g[v]:

if to == p: continue

dfsRes(to, v)

for x in range(1, k):

resA += dp[to][x - 1] * (dp[v][k - x] - dp[to][k - x - 1])

resB += dp[v][k]

Основная часть программы. Читаем количество вершин дерева n и расстояние между вершинами k.

n, k = map(int, input().split())

В списке g хранится представление дерева в виде списков смежности. Список dp используется для реализации динамического программирования.

g = [[] for _ in range(n + 1)]

dp = [[] for _ in range(n + 1)]

Читаем список ребер. Строим дерево.

for _ in range(n - 1):

a, b = map(int, input().split())

g[a].append(b)

g[b].append(a)

Первым поиском в глубину строим массив dp.

dfs(1, -1)

Подсчитываем и выводим искомый ответ.

resA, resB = 0, 0

dfsRes(1, -1)

res = resA // 2 + resB

print(res)