4104. Distance in tree
A connected
graph that contains no cycles is called a tree.
The distance
between two vertices of a tree is defined as the length (in edges) of the
shortest path connecting them.
Given a tree
with vertices and a positive integer k, calculate
the number of distinct pairs of vertices in the tree whose distance is exactly k. Note that the pairs (v, u)
and (u, v) are
considered the same.
Input. The first line contains two integers n and k (1
≤ n ≤ 50000, 1 ≤ k ≤ 500) – the
number of vertices in the tree and the required distance between vertices.
Each of the
following n – 1 lines describes an edge of
the tree in the format ai bi (1 ≤ ai, bi ≤ n, ai ≠ bi), where ai and bi are the vertices
connected by the i-th edge. All edges
are distinct.
Output. Print one
integer – the number of distinct pairs of vertices in the tree whose distance
is exactly k.
|
Sample
input |
Sample
output |
|
5 2 1 2 2 3 3 4 2 5 |
4 |
SOLUTION
dynamic programming - tree
Algorithm analysis
Let dp[v][x] denote the number of
vertices at distance x from vertex v in the subtree rooted at v. Set dp[v][0] = 1, since the only vertex at distance 0 from v is v itself.
Suppose that vertex v
has children u1, u2, .., up. Then the number of vertices at distance x from
vertex v in the subtree rooted at v is equal to the sum of the
numbers of vertices at distance x – 1
from each of the vertices u1, u2, .., up.
dp[v][x] = ![]()
Consider the subtree
rooted at vertex v. Let’s count the number of paths of length k
that lie entirely within this subtree and pass through vertex v. We
divide such paths into two groups:
·
paths that start at vertex v. Their number is equal to dp[v][k].
·
paths that pass through vertex v and whose endpoints are located in the subtrees of the children
of vertex v.
Consider a path of length k
that passes through the root of the subtree v. Let the distance from
vertex v to one end of the path be x (1 ≤ x ≤ k – 1). Suppose this end
lies in the subtree of some child u1. Then the distance from v
to the other end of the path is k − x, and this other end
can be located in any other subtree except the subtree rooted at u1.
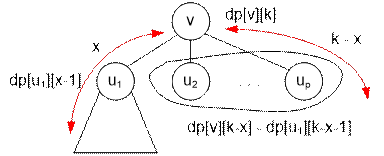
If the distance from the
first end of the path to vertex v is x, then the distance from
this end to vertex u1 is x – 1. The number of ways to choose such
a first end is dp[u1][x – 1].
The number of ways to
choose the second end of the path is equal to the number of vertices at
distance k – x from vertex v that do not belong to the subtree rooted at u1. This number is
dp[v][k – x] – dp[u1][k – x – 1]
According to the
multiplication principle, the total number of such paths is
dp[u1][x – 1] * (dp[v][k – x] – dp[u1][k – x – 1])
Thus, the total number of
such paths is
dp[v][k] + ![]()
It remains to sum the
above expression over all vertices of the tree.
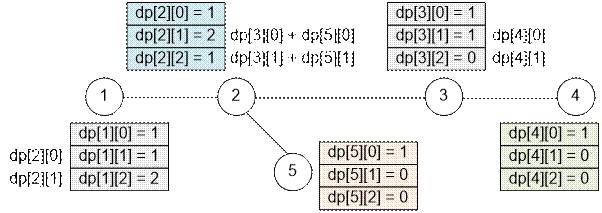
Example
Consider the tree
presented in the example.
Algorithm implementation
The array g stores
the tree representation in the form of adjacency lists. The array dp is
used to implement dynamic programming.
vector<vector<int> > g;
vector<vector<int> > dp;
The function dfs performs a depth-first search starting from vertex v.
The value p denotes the parent of vertex v. During the traversal,
the dp array is constructed.
void dfs(int
v, int p = -1)
{
Initialize the array dp[v].
dp[v].resize(k+1);
dp[v][0] = 1;
Iterate over all vertices to that can be reached from vertex v.
for (int to : g[v])
{
if (to ==
p) continue;
dfs(to,v);
for(int x = 1; x <= k; x++)
dp[v][x] += dp[to][x-1];
}
}
The function dfsRes performs a depth-first search starting from vertex v
and is intended to compute the desired answer.
void dfsRes(int
v, int p = -1)
{
for (int to : g[v])
{
if (to ==
p) continue;
dfsRes(to,v);
for(int x = 1; x < k; x++)
resA += 1LL * dp[to][x-1] * (dp[v][k-x] -
dp[to][k-x-1]);
}
resB += dp[v][k];
}
The main part of the program. Read the input data. Build the tree.
scanf("%d %d",&n,&k);
g.resize(n+1);
for (i = 0; i < n
- 1; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
g[b].push_back(a);
}
Using the first depth-first search, construct the dp array.
dp.resize(n+1);
dfs(1);
Compute and print the required answer.
resA = resB = 0;
dfsRes(1);
res = resA / 2 +
resB;
printf("%lld\n",res);
Python implementation
The function dfs performs a depth-first search starting from vertex v.
The value p denotes the parent of vertex v. During the traversal,
the dp array is constructed.
def dfs(v, p):
Initialize the array dp[v].
dp[v] = [0] * (k + 1)
dp[v][0] = 1
Iterate over all vertices to that can be reached from vertex v.
for to in g[v]:
if to == p: continue
dfs(to, v)
for x in range(1, k + 1):
dp[v][x] += dp[to][x
- 1]
The function dfsRes performs a depth-first search starting from vertex v
and is intended to compute the desired answer.
def dfsRes(v, p):
global resA, resB
for to in g[v]:
if to == p: continue
dfsRes(to, v)
for x in range(1, k):
resA += dp[to][x - 1] * (dp[v][k - x] - dp[to][k - x - 1])
resB += dp[v][k]
The main part of the program. Read the number of vertices n of the
tree, and the distance between vertices k.
n, k = map(int, input().split())
The list g stores
the tree representation using adjacency lists. The list dp is used to
implement dynamic programming.
g = [[] for _ in
range(n + 1)]
dp = [[] for _ in
range(n + 1)]
Read the list of edges. Build the
tree.
for _ in range(n - 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Using the first depth-first search, construct the dp array.
dfs(1, -1)
Compute and print the required answer.
resA, resB = 0, 0
dfsRes(1, -1)
res = resA // 2 + resB
print(res)