4107. Экстремум Эйлера

По заданному натуральному числу n найдите значение H, которое задается следующим кодом:

H = 0;

for (i = 1; i <= n; i++) {

for (j = 1; j <= n; j++) {

H = H + totient(i) * totient(j);

}

}

Функция Эйлера φ(n) или totient(n) является арифметической функцией, равной количеству натуральных чисел, меньших или равных n, взаимно простых с n. То есть если n натуральное число, то φ(n) равно количеству таких k (1 ≤ k ≤ n), что НОД(n, k) = 1.

Вход. Первая строка содержит количество тестов t (0 < t ≤ 10⁶). Каждая из следующих t строк содержит одно число n (0 < n ≤ 10⁴).

Выход. Для каждого теста выведите в отдельной строке значение H для соответствующего значения n.

Пример входа	Пример выхода
2 3 10	16 1024

РЕШЕНИЕ

Функция Эйлера

Анализ алгоритма

Перепишем указанную сумму H следующим образом:

φ(1) * φ(1) + φ(1) * φ(2) + … φ(1) * φ(n) +

φ(2) * φ(1) + φ(2) * φ(2) + … φ(2) * φ(n) +

. . .

φ(n) * φ(1) + φ(n) * φ(2) + … φ(n) * φ(n) =

φ(1) * (φ(1) + φ(2) + … φ(n)) +

φ(2) * (φ(1) + φ(2) + … φ(n)) +

. . .

φ(n) * (φ(1) + φ(2) + … φ(n)) =

= (φ(1) + φ(2) + … φ(n))²

Реализуем решето, которое вычислит все значения функции Эйлера от 1 до 10⁴ и занесет их в массив fi. Заполним массив частичных сумм sum[i] = φ(1) + φ(2) + … φ(i). Далее для каждого входного значения n выведем sum[n] * sum[n].

Пример

Рассмотрим состояние массива значений функции Эйлера fi и массива частичных сумм sum:

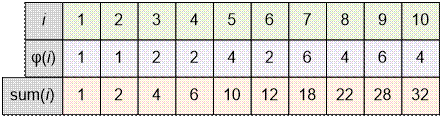
Для n = 10 ответ равен

(φ(1) + φ(2) + … φ(10))² = sum[10]² = 32² = 1024

Реализация алгоритма

Объявим рабочие массивы fi и sum, где

· fi[i] = φ(i);

· sum[i] = φ(1) + φ(2) + … φ(i)

#define MAX 10001

long long fi[MAX], sum[MAX];

Функция FillEuler заполняет массив fi[i] значениями функции Эйлера: fi[i] = φ(i), 1 ≤ i < MAX.

void FillEuler(void)

{

int i, j;

for (i = 0; i < MAX; i++) fi[i] = i;

for (i = 2; i < MAX; i++)

if (fi[i] == i)

for (j = i; j < MAX; j += i)

fi[j] -= fi[j] / i;

Вычисление частичных сумм sum[i].

sum[0] = 0; sum[1] = 1;

for(i = 2; i < MAX; i++)

sum[i] = sum[i-1] + fi[i];

}

Основная часть программы. Заполняем массивы fi и sum.

FillEuler();

Обрабатываем tests тестов.

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

Для каждого входного значения n выводим

sum[n] * sum[n] = (φ(1) + φ(2) + … φ(n))²

res = sum[n] * sum[n];

printf("%lld\n",res);

}