4211. Gas stations

Along the circular highway with a length of l there are n gas stations. If the driver wants to refuel at some point on the highway, he can drive up to any gas station, where he is happy to serve. Of course, if the fuel suddenly runs out completely, the driver will undoubtedly go to the nearest gas station, even if it means turning back.

Nevertheless, occasionally there are unlucky drivers who suddenly run out of fuel right on the road. Determine the maximum possible distance to the nearest gas station that such drivers will have to overcome on foot.

Input. The first line contains two integers: the length of the highway l (1 ≤ l ≤ 10⁵) and the number of gas stations n (1 ≤ n ≤ 10⁴). The second line contains n different integers l_i (0 ≤ l_i < l), the positions of the gas stations.

Output. Print the maximum possible distance to the nearest gas station with an accuracy of 1 decimal digit.

Sample input	Sample output
5 4 4 0 3 1	1.0

SOLUTION

greedy

Algorithm analysis

When the driver runs out of gas, he can move either forward or backward along the highway. If the distance between some neighboring gas stations is d, and the driver stops on the highway somewhere between them, then in the worst case (if the fuel runs out right in the middle), he will have to travel a distance of d / 2. The task is to find the largest distance between all neighboring gas stations and divide it by 2.

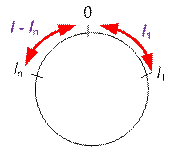
Let l₁ and l_n be the positions of the first and last gas stations, respectively. Since the highway is circular and its length is l, the distance between the first and last gas stations is l – l_n + l₁.

Example

Consider the example from the problem statement. The greatest distance is achieved between the gas stations at positions 1 and 3. It is equal to d = 2. In the worst case, the driver will have to walk a distance of d / 2 = 1 to reach the nearest gas station.

Algorithm realization

Store the positions of the gas stations in the array dist.

#define MAX 10001

int dist[MAX];

Read the input data.

scanf("%d %d",&l,&n);

for(i = 1; i <= n; i++)

scanf("%d",&dist[i]);

Sort the input positions of gas stations dist[1], …, dist[n].

sort(dist+1,dist+n+1);

We are looking for the smallest distance between adjacent gas stations, taking into account the fact that they are arranged in a circular manner. The distance between the first and last gas stations, which are considered adjacent, is equal to l – dist[n] + dist[1]. Then, when calculating the minimum, we take into account the differences dist[2] – dist[1], …, dist[n] – dist[n – 1].

res = l - dist[n] + dist[1];

for(i = 1; i < n; i++)

res = max(res,dist[i+1] - dist[i]);

Print the found answer, which is half of the smallest distance between adjacent gas stations.

printf("%.1lf\n",res/2.0);