4260. LCS – 2

Find the Longest Common Subsequence of two strings.

Input. Two strings consisting only of lowercase English letters. The length of each string does not exceed 1000 characters.

Output. Print the longest common subsequence of two strings.

Sample input	Sample output
abacaba dacabc	acab

SOLUTION

longest common subsequence

Algorithm analysis

The task of this problem is to find the longest common subsequence (LCS) of two strings and print it.

Construct an array dp, where dp[i][j] represents the length of the LCS of the substrings x_[1…i] and y_[1…j]. The value dp[n][m] will correspond to the length of the LCS of the original strings (|x| = n, |y| = m).

After computing the dp array, reconstruct the LCS by performing a reverse traversal of the matrix dp from cell (n, m) to (0, 0). At each position (i, j), we follow the next steps:

· If the characters x_i and y_j match, this character is part of the LCS. Add it to the resulting string res, and move diagonally to cell (i – 1, j – 1), continuing to build the LCS for x_{[1…i – 1]} and y_{[1…j – 1]}.

· If the characters x_i and y_j do not match, move to the cell with the larger value, either (i, j – 1) or (i – 1, j). If dp[i – 1][ j] and dp[i][j – 1] are equal, you may choose either cell.

The resulting string res will contain the longest common subsequence of x and y.

Example

Let us examine the process of finding the longest common subsequence (LCS) for two strings provided in the example.

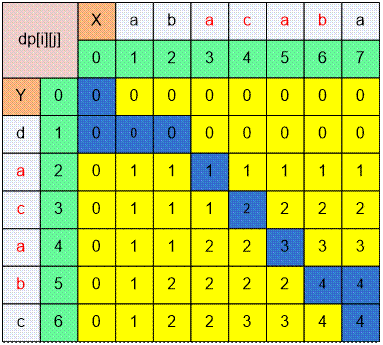
The search for the LCS starts at position (i, j) = (6, 7).

y[6] ≠ x[7]: move to any adjacent cell with the maximum value, for example, (5, 7).

y[5] ≠ x[7]: move to (5, 6).

y[5] = x[6] = ‘b’: make a diagonal move and include the character ‘b’ in the LCS.

Algorithm implementation

Declare the input strings x and y. To find their LCS, we’ll use the dp array.

#define MAX 1001

int dp[MAX][MAX];

string x, y, res;

Read the input strings. Add a space in front of each of them so that indexing starts from 1.

cin >> x; n = x.length(); x = " " + x;

cin >> y; m = y.length(); y = " " + y;

Compute the LCS.

for (i = 1; i <= n; i++)

for (j = 1; j <= m; j++)

if (x[i] == y[j])

dp[i][j] = dp[i - 1][j - 1] + 1;

else

dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

Build the LCS in the string res.

i = n; j = m;

while (i >= 1 && j >= 1)

if (x[i] == y[j])

{

res = res + x[i];

i--; j--;

}

else

{

if (dp[i - 1][j] > dp[i][j - 1])

i--;

else

j--;

}

Invert and print the resulting string.

reverse(res.begin(), res.end());

cout << res << endl;