4361. Солярий для Грибов (Hard)

И снова Михаил проводит свои эксперименты. В этот раз он решил клонировать грибы. Для этого он приготовил n спор, которые в скором времени посадит в землю и вырастит. Чтобы споры, развиваясь и увеличиваясь в размерах, не мешали друг другу, Михаил решил садить их только в целочисленных координатах. А также, чтобы ускорить процесс роста, он собирается построить большую круглую лампу, которая будет греть его подрастающие копии. Центр лампы он тоже разместит над точкой с какими-нибудь целочисленными координатами, да и радиус лампы тоже пусть будет целым. Вот только как его определить? Конечно, можно построить лампу, под которой поместится и весь лес, но на это уйдёт много лишнего времени, а времени у Михаила не так много. Так что, радиус лампы должен быть как можно меньше.

Вход. Количество спор n (0 ≤ n ≤ 3141592649625).

Выход. Выведите минимально возможный целочисленный радиус лампы, под которой поместятся все n спор.

Пример входа	Пример выхода
5	1

РЕШЕНИЕ

бинарный поиск

Анализ алгоритма

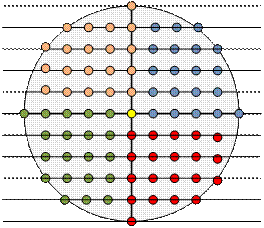
Разобьем множество точек с целочисленными координатами на пять частей как показано на рисунке: одна точка лежит в центре, остальные четыре множества равны между собой и покрывают четыре части круга. Если количество точек, лежащих в первой четверти, равно res, то общее количество точек в круге равно 4 * res + 1.

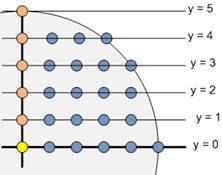
Вычислим значение res. Радиус круга равен r. Переберем значения y от 0 до r. Тогда на оси y = k (0 ≤ k ≤ r) внутри круга лежит в точности целочисленных точек. Следовательно общее число точек res в первой четверти равно

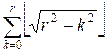
Обозначим через f(r) количество точек в круге радиуса r. Тогда

f(r) = 4 * 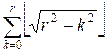+ 1

Функция f является возрастающей. В задаче следует найти минимальное r, для которого f(r) = n. Радиус лампы r ищем бинарным поиском.

Реализация алгоритма

Функция count возвращает количество точек с целочисленными координатами в круге радиуса r.

long long count(long long r)

{

long long res = 0;

double r2 = r * r;

for(long long y = 0; y <= r; y++)

res += (long long)sqrt(r2 - y*y);

return 4 * res + 1;

}

Основная часть программы. Читаем входное значение n.

scanf("%lld",&n);

Радиус круга, который покрывает как минимум n точек, ищем бинарным поиском. Изначально положим, что радиус находится в интервале [l; r] = [0; 1000000].

l = 0; r = 1000000;

while(l < r)

{

m = (l + r ) / 2;

Если количество точек в круге радиуса m меньше n, то увеличиваем левую границу интервала до m + 1 (радиуса m не хватит для покрытия n точек). Иначе уменьшаем правую.

if (count (m) < n) l = m + 1; else r = m;

}

Выводим ответ.

printf("%d\n",l);