4419. Дремучий лес

 

Чтобы помешать появлению СЭС в лагере, администрация ЛКШ перекопала единственную дорогу, соединяющую “Берендеевы поляны” с Судиславлем, теперь проехать по ней невозможно. Однако, трудности не остановили инспекцию, хотя для СЭС остается только одна возможность – дойти до лагеря пешком. Как известно, Судиславль находится в поле, а “Берендеевы поляны” – в лесу.

Судиславль находится в точке с координатами (0, 1).

“Берендеевы поляны” находятся в точке с координатами (1, 0).

Граница между лесом и полем – горизонтальная прямая y = a, где a – некоторое число (0 ≤ a ≤ 1).

Скорость передвижения СЭС по полю составляет Vp, скорость передвижения по лесу – Vf. Вдоль границы можно двигаться как по лесу, так и по полю.

Администрация ЛКШ хочет узнать, сколько времени у нее осталось для подготовки к визиту СЭС. Она попросила вас выяснить, в какой точке инспекция СЭС должна войти в лес, чтобы дойти до "Берендеевых полян" как можно быстрее.

 

Вход. В первой строке содержатся два положительных целых числа Vp и Vf (1 ≤ Vp, Vf ≤ 105). Во второй строке содержится единственное вещественное число – координата по оси Oy границы между лесом и полем a (0 ≤ a ≤ 1).

 

Выход. Выведите вещественное число с точностью не менее 8 знаков после запятой – координату по оси Ox точки, в которой инспекция СЭС должна войти в лес.

 

Пример входа

Пример выхода

5 3

0.4

0.783310604

 

 

РЕШЕНИЕ

тернарный поиск

 

Анализ алгоритма

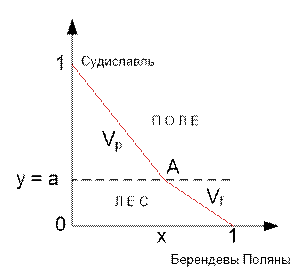
Пусть точка А пересечения границы поле / лес имеет координаты (x, a). Расстояние от Судиславля до точки А равно gp(x) = . Расстояние от точки А до Берендеевых Полян равно gf(x) = . Время движения от Судиславля до Берендеевых Полян составляет

g(x) =  +  =  +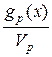

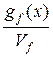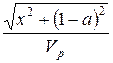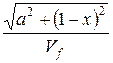
Осталось найти минимум функции g(x) на промежутке x Î [0; 1]. Что можно совершить при помощи тернарного поиска.

 

Реализация алгоритма

Определим расстояние от Судиславля до Берендеевых Полян как функцию t в зависимости от абсциссы x границы между лесом и полем.

 

double t(double x)

{

  return sqrt(x*x + (1 - a)*(1 - a)) / vp +

         sqrt(a*a + (1 - x)*(1 - x)) / vf;

}

 

Основная часть программы. Читаем входные данные.

 

scanf("%lf %lf %lf",&vp,&vf,&a);

 

Запускаем тернарный поиск для нахождения минимума функции t(x) на отрезке [0; 1].

 

Left = 0; Right = 1;

while(Right - Left >= EPS)

{

  f = Left + (Right - Left) / 3;

  g = Right - (Right - Left) / 3;

  if (t(f) < t(g)) Right = g; else Left = f;

}

 

Выводим ответ – абсциссу точки, в которой инспекция СЭС должна войти в лес.

 

printf("%.9lf\n",Left);