4419. Dense forest
To prevent the appearance of
sanitary inspection in the camp, the LKSH administration dug the only road
connecting the “Berendevy polyany” with Sudislavl, so now it is impossible to
travel along it. However, the difficulties did not stop the inspection, for it
remains only one possibility – to reach the camp on foot. As you know,
Sudislavl is in the field, and “Berendevy polyany” are in the forest.
·
Sudislavl is located at the point with coordinates (0, 1).
·
“Berendevy polyany” are located at the point with coordinates
(1, 0).
·
The border between the field and forest is a horizontal line y = a, where a is some
number (0 ≤ a ≤ 1).
·
The speed of sanitary inspection through the field is Vp, the speed through the
forest is Vf. Along the border it is
allowed to move either by forest or by field.
The LKSH administration want
to know how much time left to prepare for sanitary inspection visit. It asked
you to find out at what point the sanitary inspection should enter into the
forest to reach “Berendevy polyany” as fast as possible.
Input. First line contains two
positive integers Vp and Vf (1
≤ Vp, Vf ≤ 105). Second line contains one
real number – the Oy coordinate of the border between the forest and field
a (0 ≤ a ≤ 1).
Output. Print one real number with
accuracy of no less than 8 digits after the decimal point – the Ox coordinate
of the point at which the sanitary inspection will enter the forest.
|
Sample input |
Sample output |
|
5 3 0.4 |
0.783310604 |
SOLUTION
ternary search
Algorithm analysis
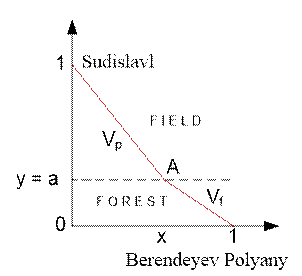
Let the point A
of intersection of the border field / forest have coordinates (x, a).
The distance from Sudislavl to point A equals to gp(x) = ![]() . The distance from point A to Berendeyev Polyany is gf(x) =
. The distance from point A to Berendeyev Polyany is gf(x) = ![]() . The
travel time from Sudislavl to Berendeyev Polyany is
. The
travel time from Sudislavl to Berendeyev Polyany is
g(x) = 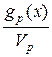 +
+ 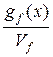 =
=  +
+ 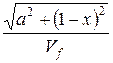
It remains to find the minimum of the function g(x) on the interval x Î [0; 1]. This can be done with ternary search.
Algorithm realization
Determine the
distance from Sudislavl to Berendeyev Polyany as a function t depending on the abscissa x of the border between the forest and the field.
double t(double x)
{
return
sqrt(x*x + (1 - a)*(1 - a)) / vp +
sqrt(a*a + (1 - x)*(1 - x)) / vf;
}
The main part of the program. Read the input data.
scanf("%lf %lf %lf",&vp,&vf,&a);
Run ternary search
to find the minimum of the function t(x) on the segment
[0; 1].
Left
= 0; Right = 1;
while(Right
- Left >= EPS)
{
f = Left + (Right - Left) / 3;
g = Right - (Right - Left) / 3;
if (t(f) <
t(g)) Right = g; else Left = f;
}
Print the answer – the abscissa of the point where the sanitary inspection should enter
the forest.
printf("%.9lf\n",Left);