4439. Exponentiation

Find the value of xⁿ.

Input. Two positive integers x and n.

Output. Print the value of xⁿ, if it does not exceed 10¹⁸.

Sample input	Sample output
2 10	1024

SOLUTION

exponentiation

Algorithm analysis

How to compute xⁿ faster than O(n)? For example,

x¹⁰ = (x⁵)² = (x * x⁴)² = (x * (x²) ²)²

It can be noted that x²ⁿ = (x²)ⁿ, for example x¹⁰⁰ = (x²)⁵⁰.

For odd powers, we use the formula x²ⁿ⁺¹ = x * x²ⁿ, for example x¹¹ = x * x¹⁰.

The following recursive formula gives us an O(log₂n) solution:

=

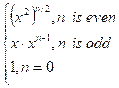
In an iterative implementation, the case when x = 1 and n is a large integer should be handled separately. For example, when x = 1 and n = 10¹⁸, computing xⁿ would require 10¹⁸ iterations, which would result in a Time Limit.

Algorithm realization

The function f computes the value of xⁿ.

long long f(long long x, long long n)

{

if (n == 0) return 1;

if (n % 2 == 0) return f(x * x, n / 2);

return x * f(x, n - 1);

}

The main part of the program. Read the input data.

scanf("%lld %lld",&x,&n);

Compute and print the answer xⁿ.

res = f(x,n);

printf("%lld\n",res);