4469. Domino

Find the number of ways to completely tile a rectangle of size 2 × n with dominoes of size 2 × 1. Coverings that coincide with themselves under symmetries (rotations or reflections) are considered different.

Input. One integer n (0 < n < 65536).

Output. Print the number of ways to tile the rectangle with dominoes.

Sample input 1	Sample output 1
1	1
Sample input 2	Sample output 2
4	5

SOLUTION

Fibonacci numbers

Algorithm analysis

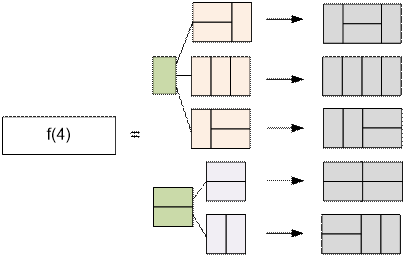
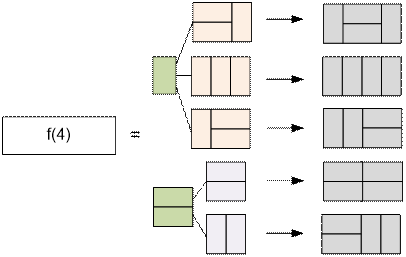
Let f(n) denote the number of ways to tile a 2 × n rectangle with 2 × 1 dominoes. It is clear that

· f(1) = 1, one vertical domino;

· f(2) = 2, either two vertical dominoes or two horizontal dominoes.

Consider the algorithm for computing f(n):

· we can place one domino vertically, after which the remaining rectangle of length n – 1 can be tiled in f(n – 1) ways,

· or we can place two dominoes horizontally, after which the remaining rectangle of length n – 2 can be tiled in f(n – 2) ways.

Thus, we obtain the recurrence relation:

f(n) = f(n – 1) + f(n – 2)

Therefore, f(n) is a Fibonacci number.

Algorithm implementation

Since n < 65536, long arithmetic or Java programming language should be used.

import java.util.*;

import java.math.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

BigInteger a = new BigInteger("1"), b = a;

for(int i = 0; i < n; i++)

{

BigInteger temp = a.add(b);

a = b;

b = temp;

}

System.out.println(a);

con.close();

}

}

Python implementation

Increase the limit to the required value (for example, 100,000 digits).

import sys

sys.set_int_max_str_digits(100000)

Read the input value n.

n = int(input())

Process the base cases.

if n == 1:

print(1)

elif n == 2:

print(2)

else:

Compute the n-th Fibonacci number.

f1, f2 = 1, 2

for i in range(n - 2):

temp = f1 + f2

f1, f2 = f2, temp

Print the answer.

print(f2)