4483. Козленок, который учился считать

 

Козленок работает контроллером на кораблике-пароме. Его задача следить, чтобы паром не утонул от превышения грузоподъемности. Сегодня на кораблик осталось всего два билета, кроме того кораблик может выдержать дополнительно еще k килограмм. В этом лесу всего одна длинная дорога, вдоль которой живут звери. Помогите козленку узнать, сможет ли он на определенном участке леса найти двух пассажиров.

 

Вход.  В первой строке содержится два числа n (2 ≤ n ≤ 106) и k (1 ≤ k ≤ 109), количество зверей в лесу и оставшаяся грузоподъемность парома соответственно. Во второй строке находится n чисел – массы каждого из зверей. Далее следует количество запросов m. В следующих m (1 ≤ m ≤ 105) строках находится по три числа – тип запроса, l и r (если тип запроса 1, то 1 ≤ l < r ≤ n, иначе 1 ≤ l ≤ n, 1 ≤ r ≤ 109).

 

Выход. Для каждого запроса с типом 1 выведите строку “Yes”, если козленок сможет найти двух пассажиров на промежутке [l; r] и “No”, если не сможет. Каждый запрос с типом 2 означает, что зверь под номером l изменил свою массу и теперь весит r килограмм.

 

Пример входа

Пример выхода

6 9

1 3 1 6 6 7

8

1 1 6

1 1 2

2 4 7

1 4 5

1 5 6

2 1 7

2 3 8

1 1 6

Yes

Yes

No

No

Yes

 

 

РЕШЕНИЕ

структуры данных - дерево отрезков, единичная модификация

 

Анализ алгоритма

Можно построить дерево отрезков, поддерживающее два минимума. Однако нас в задаче интересуют на сами минимумы на отрезках, а само существование двух чисел с суммой не большей k.

В листья дерева отрезков занесем веса пассажиров. В остальных вершинах дерева будем поддерживать значения согласно следующих правил:

·        если сумма чисел в левом и правом сыне вершины не больше чем k, то для текущего интервала [l; r] существуют искомые два пассажира. В вершину, которой соответствует интервал [l; r], занесем 0.

·        иначе в вершину заносим минимум ее сыновей.

Выполнение запросов: если минимум на отрезке [l; r] равен 0, то существуют требуемые два пассажира, ответ “Yes”. Иначе ответ “No”.

 

Пример

Построим дерево для k = 9 и весов пассажиров 7, 3, 8, 7, 6, 7.

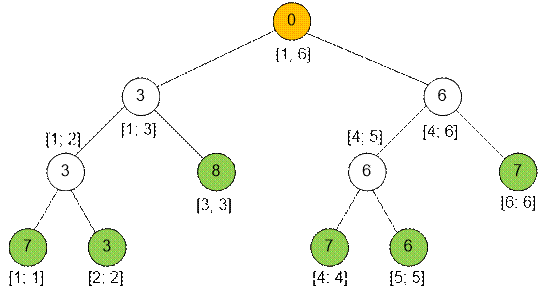
Из фундаментальных отрезков только вершина [1; 6] будет содержать 0.

 

Реализация алгоритма

Объявим массив SegTree для хранения дерева отрезков. Массы зверей храним в массиве a.

 

#define MAX 1000010

#define MAX_INT 1050000000

int SegTree[4*MAX];

int a[MAX];

 

Функция f реализует слияние сыновей вершин дерева отрезков. Дерево отрезков поддерживает операцию минимума. Но если сумма значений в левом и правом сыне не больше k, то возвращаем 0. Если один из сыновей уже содержит 0, но на его отрезке существуют два искомых пассажира, поэтому возвращаем 0.

 

int f(int a, int b)

{

  if (a == 0 || b == 0 || a + b <= k) return 0;

  return min(a,b);

}

 

На вход функции BuildTree построения дерева отрезков передается номер текущей вершины дерева v и границы отрезка lpos и rpos, соответствующие вершине v. При слиянии сыновей используем функцию f.

 

void BuildTree(int v, int lpos, int rpos)

{

  if (lpos == rpos)

    SegTree[v] = a[lpos];

  else

  {

    int mid = (lpos + rpos) / 2;

    BuildTree(2 * v, lpos, mid);

    BuildTree(2 * v + 1, mid + 1, rpos);

    SegTree[v] = f(SegTree[2 * v], SegTree[2 * v + 1]);

  }

}

 

Функция Query реализует запрос на отрезке [left; right]. Вершине v соответствует отрезок [lpos, rpos]. Если на отрезке [left, right] существуют два пассажира с суммарной массой не больше k, то функция Query возвращает 0. Иначе она возвращает наименьший вес пассажира на отрезке [left; right].

 

int Query(int v, int lpos, int rpos, int left, int right)

{

  if (left > right) return MAX_INT;

  if ((lpos == left) && (rpos == right)) return SegTree[v];

  int mid = (lpos + rpos) / 2;

  return f(Query(2 * v, lpos, mid, left, min(right, mid)),

          Query(2 * v + 1, mid + 1, rpos, max(left, mid + 1), right));

}

 

Функция Update присваивает элементу с индексом pos значение val. Вершине v соответствует отрезок [lpos, rpos].

 

void Update(int v, int lpos, int rpos, int pos, int val)

{

  if (lpos == rpos)

    SegTree[v] = val;

  else

  {

    int mid = (lpos + rpos) / 2;

    if (pos <= mid) Update(2 * v, lpos, mid, pos, val);

    else Update(2 * v + 1, mid + 1, rpos, pos, val);

    SegTree[v] = f(SegTree[2 * v], SegTree[2 * v + 1]);

  }

}

 

Основная часть программы. Читаем массы зверей в массив a, начиная с нулевого индекса.

 

scanf("%d %d",&n,&k);

for (i = 0; i < n; i++) scanf("%d",&a[i]);

 

Строим дерево отрезков по элементам массива a[0..n – 1].

 

BuildTree(1,0,n-1);

 

Последовательно обрабатываем запросы.

 

scanf("%d",&q);

for (j = 0; j < q; j++)

{

  scanf("%d %d %d",&t,&l,&r);

  if (t == 1)

  {

    int Res = Query(1,0,n-1,l-1,r-1);

    if (Res == 0) printf("Yes\n"); else printf("No\n");

  }

  else

    Update(1,0,n-1,l-1,r) ;

}