4486. Чебурашка и
крокодил Гена
Когда Чебурашка
и крокодил Гена не знают, чем заняться, они играют в различные интересные игры.
Сегодня Гена придумал новую игру, которая, по его мнению, поможет Чебурашке
лучше освоить арифметику.
Правила игры
просты: Гена берет n дощечек, пронумерованных от 1 до n, и
записывает на них какие-то числа. Затем он называет два числа l и r,
а Чебурашка должен вычислить сумму всех чисел на дощечках с номерами от l
до r.
Чтобы Чебурашка
не запомнил все возможные ответы, Гена иногда изменяет значения чисел. В
частности, он заменяет все числа на промежутке [l, r], записывая на этих
дощечках последовательность чисел от 1 до r
– l + 1 в порядке возрастания.
Чебурашка пока
не очень хорошо считает, поэтому просит Вас написать программу, которая поможет
ему выполнять вычисления.
Вход. В первой строке содержится число n (1 ≤ n
≤ 106) – количество дощечек.
Во второй строке записаны n
чисел – начальные
значения, написанные на дощечках (каждое число не превышает 109).
Далее следует число m (1 ≤ m
≤ 105) – количество запросов.
Затем идут m строк, каждая из которых описывает один из
двух типов запросов. Первое число в строке содержит вид запроса t (1 ≤ t ≤ 2).
·
Если t = 1, после него следуют два
числа l и r. Вам следует вычислить сумму всех
чисел на дощечках с номерами от l до r.
·
Если t = 2, после него следуют два
числа l и r. Это означает, что числа на дощечках с
номерами от l до r заменяются последовательностью 1, 2, … , r – l + 1.
Гарантируется, что все
запросы заданы корректно, а нумерация дощечек начинается с единицы.
Выход. Для каждого запроса типа 1 выведите одно
число – сумму значений на дощечках в заданном промежутке [l,
r].
|
Пример
входа |
Пример
выхода |
|
5 5 3 2 4 5 5 1 1 5 1 2 3 2 1 5 2 2 5 1 1 5 |
19 5 11 |
РЕШЕНИЕ
структуры
данных - дерево отрезков
Анализ алгоритма
Построим дерево
отрезков, поддерживающее операцию суммирования. В каждой вершине (фундаментальном отрезке [a; b]) дополнительно будем хранить значение left. Если left > 0, то в вершине [a; b] имеется
отложенная операция: всем вершинам ее поддерева следует присвоить значения left, left + 1, …, left + b – a. Изначально left во всех вершинах равно нулю.
Рассмотрим
процедуру проталкивания значений. Пусть запрос q(x,
y) частично пересекает оба поддерева, то
есть x ≤ m < y. В этом случае:
·
Для левого сына устанавливаем left = 1.
·
Для правого сына значение left устанавливаем на 1
большим длины отрезка [x; m].

Если a ≠ x (b ≠ y), то значение left следует проталкивать дальше.
Если x ≥ m + 1 (отрезок запроса полностью лежит в правом поддереве),
то значение left для левого сына остается равным 0.
Пусть запрос q(x, y)
покрывается набором фундаментальных отрезков [a1,
b1], [a2, b2],
…, [ak, bk]. Тогда значение left для отрезка [ai, bi]
установим равным
1 + сумма длин
всех предыдущих
отрезков
[aj, bj], для которых j
< i
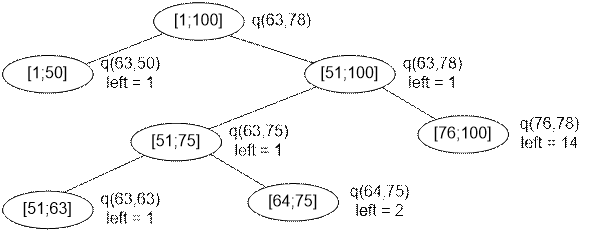
Например, пусть дерево построено на отрезке
[1..8], а запрос q(2, 7) покрывает следующие фундаментальные отрезки:

Пример
Рассмотрим следующий тест:
5
5 3 2 4 5
2
2 2 5
1 1 3
Возле каждой вершины в прямоугольнике записана сумма на
отрезке.
Реализация алгоритма
Объявим массив SegTree для хранения дерева отрезков.
struct node
{
long long summa;
int left;
};
vector<node> SegTree;
Функция BuildTree строит дерево
отрезков.
void BuildTree(int v, int lpos, int rpos)
{
if (lpos == rpos)
SegTree[v].sum = a[lpos];
else
{
int mid = (lpos + rpos) / 2;
BuildTree(2 * v, lpos, mid);
BuildTree(2 * v + 1, mid + 1, rpos);
SegTree[v].sum = SegTree[2 * v].sum + SegTree[2 * v + 1].sum;
}
}
Функция Sum вычисляет сумму чисел от a до b.
long long
Sum(int a, int
b)
{
return 1LL *
(a + b) * (b - a + 1) / 2;
}
Функция Push выполняет
проталкивание значения left из вершины v в ее сыновья. Производится пересчет суммы sum в сыновьях.
void Push(int v, int lpos, int mid, int rpos)
{
if (SegTree[v].left)
{
SegTree[2 * v].left = SegTree[v].left;
SegTree[2 * v].sum = Sum(SegTree[2 * v].left,
SegTree[2 * v].left + mid - lpos);
SegTree[2 * v + 1].left = SegTree[v].left + mid - lpos + 1;
SegTree[2 * v + 1].sum = Sum(SegTree[2 * v + 1].left,
SegTree[2 * v + 1].left + rpos - mid - 1);
SegTree[v].left = 0;
}
}
Функция Update заполняет промежуток [left; right] последовательностью значений from, from + 1, from + 2, ….
void Update(int v, int lpos, int rpos, int left, int right, int from)
{
if (left > right) return;
if ((lpos == left) && (rpos == right))
{
SegTree[v].left = from;
SegTree[v].sum = Sum(from, from + right - left);
return;
}
int mid = (lpos + rpos) / 2;
int midval = mid - left + 1;
Если отрезок запроса [left; right] полностью
лежит в правом поддереве [mid + 1; rpos], то передаем правому сыну значение from без изменений (при этом midval
устанавливаем равным нулю).
if (midval < 0) midval =
0;
Push(v, lpos, mid, rpos);
Update(2 * v, lpos, mid, left, min(mid, right), from);
Update(2 * v + 1, mid + 1, rpos, max(left, mid + 1),
right, from + midval);
SegTree[v].sum = SegTree[2 * v].sum + SegTree[2 * v + 1].sum;
}
Функция Summa возвращает сумму чисел на отрезке [left; right].
long long Summa(int v, int lpos, int rpos, int Left, int Right)
{
if (Left > Right) return 0;
if ((lpos == Left) && (rpos == Right)) return SegTree[v].sum;
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos);
return Summa(2 * v, lpos, mid, Left, min(mid, Right)) +
Summa(2 * v + 1, mid + 1, rpos, max(Left, mid + 1), Right);
}
Основная часть программы. Читаем
входной массив чисел.
scanf("%d", &n);
a.resize(n
+ 1);
for(i = 1; i <= n; ++i)
scanf("%d",
&a[i]);
Строим дерево отрезков.
SegTree.resize(4
* n);
BuildTree(1,
1, n);
Последовательно обрабатываем q запросов.
scanf("%d", &q);
for(i = 0; i < q; ++i)
{
scanf("%d %d
%d", &type, &l, &r);
if(type == 1)
printf("%lld\n",
Summa(1,1,n,l,r));
else
Update(1,1,n,l,r,1);
}