4491. Трое из Простоквашино

- Дядя Федор, Дядя Федор, я научился строить дерево отрезков.

- Подожди, Шарик, я занят.

- Ну Дядя Федор, ну смотри какой я код написал:

int build(int v, int left, int right)

{

if (left == right)

{

t[v] = a[left];

return 0;

}

int mid = (left+right) / 2;

build(v*2, left, mid);

build(v*2+1, mid+1, right);

t[v] = max(t[v*2], t[v*2+1]);

return 0;

}

int get_max(int v, int left, int right, int lpos, int rpos)

{

if (left == lpos && right == rpos)

return t[v];

if (lpos > rpos)

return -1;

int mid = (left+right) / 2;

return max(get_max(v*2, left, mid, lpos, min(rpos, mid)),

get_max(v*2+1,mid+1,right,max(lpos,mid+1),rpos));

}

- Ну хорошо, Шарик, раз ты так хорошо разобрался с этой темой, давай я тебе дам массив из n неотрицательных чисел и число k, а ты мне скажешь сколько существует таких пар l; r (1 ≤ l ≤ r ≤ n), что функция, вызванная следующим образом

get_max(1, 1, n, l, r)

вернет значение равное k. Можно считать, что перед этим была вызвана функция

build(1, 1, n)

- Хорошо, Дядя Федор!

Вход.  В первой строке находятся число n (1 ≤ n ≤ 10⁶) – количество элементов в массиве и k (1 ≤ k ≤ 10⁹) – значение, которое должна вернуть функция. В следующей строке находится n неотрицательных чисел, не превышающих 10⁹ – элементы массива.

Выход. Выведите единственное число – ответ на задачу.

Пример входа	Пример выхода
5 3 1 2 3 2 3	11

РЕШЕНИЕ

линейный алгоритм

Анализ алгоритма

Обозначим через а входной массив. Если a[i] > k для некоторого i, то не существует таких l, r, что l ≤ i ≤ r, для которых max(l, r) = k.

Если max(l, r) = k, то на промежутке [l; r] существует число, равное k, а все остальные числа не больше k.

Пусть [Left, Right] – отрезок массива, на котором максимум равен k, причем a_Right = k. Изначально установим Left = Right = 0 (левая граница установлена на начало массива, правая граница при равенстве 0 считается неопределенной). Пусть i – текущий просматриваемый элемент (i > Right). Тогда:

· если a_i = k (при этом подразумевается, что все значения от a_Right+1 до a_i-1 меньше k), то на всех отрезках вида [j; i], где Left ≤ j ≤ i, максимум будет также равен k. Устанавливаем Right = i.

· если a_i < k, то на всех отрезках вида [j; i], где Left ≤ j ≤ Right, максимум будет также равен k.

· если a_i > k, то Left устанавливаем равным i + 1, а Right делаем неопределенным (равным 0).

Пример

Пусть k = 3. Массив изображен ниже.

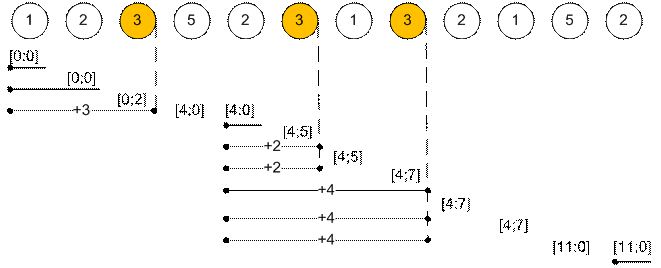
Реализация алгоритма

Входную последовательность храним в массиве а.

#define MAX 1000001

int a[MAX];

Читаем входные данные.

scanf("%d %d",&n,&k);

for(i = 0; i < n; i++) scanf("%d",&a[i]);

Подсчитываем количество требуемых интервалов согласно приведенному в анализе задаче алгоритму.

Left = Right = Res = 0;

for(i = 0; i < n; i++)

{

if(a[i] == k) Res += i - Left + 1, Right = i; else

if(a[i] < k && Right != 0) Res += Right - Left + 1;

else if(a[i] > k) Right = 0, Left = i + 1;

}

Выводим ответ.

printf("%lld\n",Res);