4516. Деревья в саду

Центральный сад страны Олимпия настолько большой, что один садовник не в силах его обслуживать. Было принято решение разделить сад на две части. Определенные деревья будут отнесены к первой части, а оставшиеся – ко второй. Одна из частей сада может остаться пустой.

Между каждой парой деревьев в саду протоптаны тропинки. Когда садовники идут от дерева к дереву, они обязательно идут по тропинке соединяющей непосредственно эти два дерева. Длина тропинки одинакова при перемещении в обе стороны.

Для упрощения работы садовников, разделение решили проводить так, чтобы длина самой длинной тропинки между парой деревьев, принадлежащих одной и той же части, была минимальна.

Напишите программу, которая по информации о длинах тропинок между всеми парами деревьев находит длину самой длинной тропинки между деревьями из одной части сада, при оптимальном разделении сада на части.

Вход. Первая строка содержит целое число n (2 ≤ n ≤ 1000) – количество деревьев в саду. Каждая i-ая из последующих (n – 1) -ой строк содержит n – i чисел, которые последовательно представляют длины тропинок между i-ым деревом и деревьями с i + 1-го до n-го. Все числа целые, неотрицательные, и не превышают 10⁶.

Выход. Вывести одно целое число – минимальную для всех возможных разбиений сада длину самой длинной тропинки между деревьями в одной из частей сада.

Пример входа	Пример выхода
3 1 5 1	1

РЕШЕНИЕ

графы - поиск в глубину + бинарный поиск

Анализ алгоритма

В задаче требуется поставить в соответствие каждому дереву одного садовника, который будет его обслуживать.

Рассмотрим следующую подзадачу: можно ли разбить деревья сада между двумя садовниками таким образом, чтобы не существовало тропинок (по которым каждый из садовников будет ходит в отдельности) длины больше x. Если мы научимся отвечать на этот вопрос, то дальше ищем минимальное значение x (ответ к задаче), при котором существует такое разбиение, бинарным поиском.

Построим граф, в котором присутствуют только ребра длины больше x. Если такой граф является двудольным, то каждое множество деревьев будет обслуживать один из садовников. И ни один из садовников не будет иметь в своем распоряжении тропинки длиной больше x.

Пример. Пусть изначально имеется следующий граф:

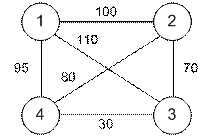
Попробуем разбить деревья сада между двумя садовниками таким образом, чтобы не существовало тропинок длины строго больше x = 70. Для этого следует проверить граф, содержащий лишь ребра величины больше 70, на двудольность:

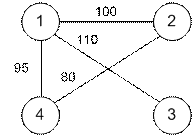
Такой граф не является двудольным. Рассмотрим граф, для которого x = 80. Такой граф будет двудольным:

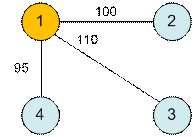
Можно заметить, что при x < 80 в графе из ребер с весами большими x, всегда будет цикл нечетной длины (1 – 2 – 4). Поэтому ответом будет значение 80.

Реализация алгоритма

Объявим массивы для работы с графом. Граф храним в виде весовой матрицы.

.

#define MAX 1010

int g[MAX][MAX], used[MAX];

Поиск в глубину из вершины v. Красим вершину v цветом Color. Проверяем, является ли граф двудольным, если разрешено проходить лишь по ребрам, веса которых больше Value. То есть можно ли разбить граф на две доли так, чтобы все ребра с весом больше Value соединяли вершины из разных долей.

void dfs(int v, int Color, int Value)

{

if (Error) return;

used[v] = Color;

for(int i = 1; i<= n; i++)

if (g[v][i] > Value)

if (!used[i]) dfs(i,3-Color,Value); else

if (used[i] == used[v]) Error = 1;

}

Функция CanDivide возвращает 1, если возможно разделить сад так, чтобы по тропинкам длины Value не ходили садовники. Поиск в глубину запускаем как на несвязном графе, так как реально он будет вестись только по ребрам, вес которых больше Value.

int CanDivide(int Value)

{

memset(used,0,sizeof(used));

Error = 0;

for(int i = 1; i <= n; i++)

{

if (!used[i]) dfs(i,1,Value);

if (Error) return 0;

}

return 1;

}

Основная часть программы. Читаем входные данные. Ищем длину минимального mind и максимального maxd ребра.

scanf("%d", &n);

mind = 2e9; maxd = 0;

memset(g,0,sizeof(g));

for(i = 1; i < n; i++)

for(j = i + 1; j <= n; j++)

{

scanf("%d", &g[i][j]);

g[j][i] = g[i][j];

if (g[i][j] > maxd) maxd = g[i][j];

if (g[i][j] < mind) mind = g[i][j];

}

Если имеется два дерева (n = 2), то ответ 0. Этот случай следует обработать отдельно.

if (n == 2) maxd = 0; else

Иначе запускаем бинарный поиск на промежутке [mind, maxd].

while(mind < maxd)

{

int Middle = (mind + maxd) / 2;

if (CanDivide(Middle)) maxd = Middle;

else mind = Middle + 1;

}

Выводим ответ.

printf("%d\n",maxd);