4529. Последняя цифра числа Фибоначчи

Найдите последнюю цифру k-го числа Фибоначчи.

Напомним, что числа Фибоначчи определяются следующими рекуррентными соотношениями:

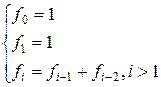
Вход. В каждой строке задано одно целое число k (0 ≤ k ≤ 9223372036854775807).

Выход. Для каждого теста выведите в отдельной строке последнюю цифру k-го числа Фибоначчи.

Пример входа	Пример выхода
0 1 2 37 135 23	1 1 2 9 7 8

РЕШЕНИЕ

Числа Фибоначчи

Анализ алгоритма

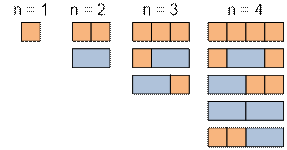
Рассмотрим следующую задачу. Сколькими способами можно замостить таблицу 1 × n костями домино 1 × 2 и квадратами 1 × 1? Пусть это количество равно f(n). Очевидно, что f(1) = 1, f(2) = 2.

Если первую ячейку таблицы покрыть квадратом, то далее останется замостить таблицу 1 × (n – 1), что можно совершить f(n – 1) способами. Если первую и вторую ячейку таблицы покрыть костью домино, то далее останется замостить таблицу 1 × (n – 2), что можно совершить f(n – 2) способами.

Таким образом f(n) = f(n – 1) + f(n – 2), то есть являются числами Фибоначчи.

Пусть имеется таблица 1 × (n + m). Ее можно покрыть f(n + m) способами. Рассмотрим сначала покрытия, в которых нет домино, покрывающего ячейки n и n + 1.

Тогда первые n ячеек можно покрыть квадратами и домино f(n) способами, а последние m ячеек можно покрыть f(m) способами. То есть всю таблицу можно покрыть f(n) * f(m) способами.

Теперь рассмотрим покрытия, в которых одна кость домино покрывает ячейки n и n + 1. Таких покрытий будет f(n – 1) * f(m – 1).

Резюмируя сказанное, получим что

f(n + m) = f(n) * f(m) + f(n – 1) * f(m – 1),

f(1) = 1, f(2) = 2.

Выведем некоторые тождества из указанной рекурренстности:

· если m = n, то f(2n) = f(n) * f(n) + f(n – 1) * f(n – 1),

· если m = n + 1, то f(2n + 1) = f(n) * f(n + 1) + f(n – 1) * f(n)

Вычисляя числа Фибоначчи при помощи указанных соотношений, получим логарифмическую сложность.

Реализация алгоритма

Поскольку индексы вычисляемых чисел Фибоначчи имеют порядок 10¹⁸, то использовать линейный массив такого размера для запоминания невозможно. Для запоминания вычислений будем использовать структуру данных map.

map<long long, long long> fib;

Вычисление n-го числа Фибоначчи.

long long f(long long n)

{

if (n <= 1) return 1;

if (n == 2) return 2;

if (fib[n] != 0) return fib[n];

long long k = n / 2;

if (n % 2 == 0)

return fib[n] = (f(k - 1) * f(k - 1) + f(k) * f(k)) % 10;

return fib[n] = (f(k) * (f(k - 1) + f(k + 1))) % 10;

}

Основная часть программы. Читаем входное значение n, выводим n-ое число Фибоначчи f(n).

while (scanf("%lld", &n) == 1)

printf("%lld\n", f(n));