4529. Fibonacci numbers: the last
digit
Find
the last digit of the k-th
Fibonacci number.
Fibonacci
numbers are defined by the following recurrence relations:
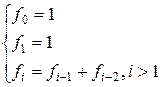
Input. Each
line contains a single number k (0 ≤ k ≤ 9223372036854775807).
Output. For
each test case print in a separate line the last digit of the k-th Fibonacci number.
|
Sample input |
Sample output |
|
0 1 2 37 135 23 |
1 1 2 9 7 8 |
SOLUTION
Fibonacci numbers
Algorithm
analysis
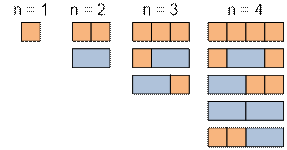
Consider the next problem. In how many ways is it possible to
cover the strip 1 × n with domino of size 1
× 2 and squares of
size 1 × 1? Let this number of ways be f(n). Obviously
that f(1) = 1, f(2) = 2.
If we cover the first cell of the
table with a square, then
we need to cover the strip 1 × (n – 1), it can be done in f(n – 1) ways. If
we cover the first and the second cell of the table with a domino, then we need to cover the strip 1 × (n – 2), it can be done in f(n – 2) ways.
![]()
Thus f(n) = f(n – 1) + f(n – 2), so f(n) are Fibonacci numbers.
Let we have a table 1 × (n + m). It can be covered in f(n + m) ways. First we consider the coverings without
domino that covers the cells n and n + 1.

Then the first n cells can be
covered with squares and dominos in f(n) ways, and the last m cells
can be covered with f(m) ways. That is, the
entire table can be covered in f(n) * f(m) ways.
Now consider the coverings where one
domino covers the cells n and n + 1. We have f(n –
1) * f(m –
1) such coverings.

Summarizing, we
get that
f(n + m) = f(n) * f(m) + f(n –
1) * f(m –
1),
f(1) = 1, f(2) = 2.
Let's obtain some identities
from the indicated recurrence:
·
if
m = n, then f(2n) = f(n) * f(n) + f(n –
1) * f(n –
1),
·
if m = n + 1, then f(2n + 1) = f(n) * f(n
+ 1) + f(n – 1) * f(n)
Calculating the Fibonacci numbers using the above
relations, we obtain the logarithmic complexity O(log2n).
Algorithm
realization
Since the
indices of the calculated Fibonacci numbers have the order of 1018, it is impossible to use a
linear array of this size for memorization. To memorize the results we’ll
use the map data structure.
map<long long, long long> fib;
The calculation of the n-th
Fibonacci number.
long long f(long long n)
{
if (n <= 1) return 1;
if (n == 2) return 2;
if (fib[n] != 0) return fib[n];
long long k = n / 2;
if (n % 2 == 0)
return fib[n] = (f(k - 1) *
f(k - 1) + f(k) * f(k)) % 10;
return fib[n] = (f(k) * (f(k
- 1) + f(k + 1))) % 10;
}
The main part of the program. Read the input value n and print the n-th
Fibonacci number f(n).
while (scanf("%lld", &n) == 1)
printf("%lld\n", f(n));