4538. Вася и шары
Недавно Вася
узнал, что с шарами можно играть в очень занимательную игру. В этой игре
требуется укладывать шары в виде различных геометрических фигур и тел. Пока
Вася занимается укладкой шаров в виде равностороннего треугольника. Но вот незадача:
иногда Васе не хватает наличных шаров, и он хочет знать, какова наибольшая
сторона такого треугольника, для которого хватит Васиных шаров? Помогите Васе,
напишите для него программу, которая будет вычислять n – длину стороны равностороннего треугольника для заданного
количества шаров k.
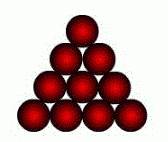
Ниже приведён
пример укладки шаров в виде равностороннего треугольника:
Вход. Натуральное число k
(0 ≤ k ≤ 2 *108)
– имеющееся количество шаров.
Выход. Вывести число n
– ответ задачи.
|
Пример
входа |
Пример
выхода |
|
5 |
2 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
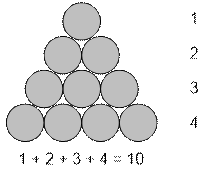
Если n – длина стороны треугольника, то для
полной его укладки требуется 1 + 2 + … + n
= n * (n + 1) / 2 шаров.
В наличии
имеется k шаров. Решим уравнение n * (n
+ 1) / 2 = k и округлим неотрицательный
корень вниз до ближайшего целого.
Решим квадратное
уравнение: n2 + n – 2k
= 0, d = 1 + 8k, n = 
.
Ответом будет
значение 
.
Реализация алгоритма
Читаем значение k. Вычисляем и выводим ответ.
scanf("%d",&k);
n = int((-1 + sqrt(1.0 + 8*k)) / 2.0);
printf("%d\n",n);
Реализация
алгоритма – бинарный поиск
#include <stdio.h>
long long n, k, l, r, mid, res;
long long f(long long n)
{
return n * (n + 1) /
2;
}
int my_upper_bound(int start, int end, int x)
{
while (start <
end)
{
int mid = (start +
end) / 2;
if (f(mid) > x)
end = mid;
else
start = mid + 1;
}
return start;
}
int main()
{
scanf("%lld", &k);
// find min n:
f(n) >= k
if (k == 0) res =
0;
else if (k == 1) res =
1;
else res =
my_upper_bound(0, k, k) - 1;
printf("%d\n", res);
}
Реализация алгоритма – O(sqrt(n))
#include <stdio.h>
long long n, k, res;
long long f(long long n)
{
return n * (n + 1) /
2;
}
int main()
{
scanf("%lld",
&k);
// find
min n: f(n) >= k
n = 0;
while (f(n)
<= k) n++;
printf("%d\n", n);
}