4556. Подсчет треугольников
Определим УРОВЕНЬ
треугольника следующим изображением:
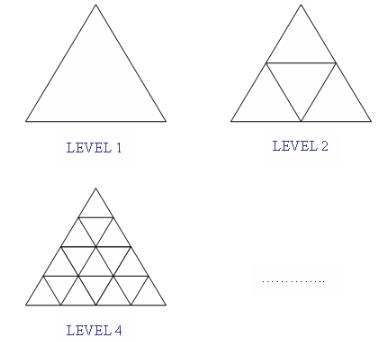
Вам следует подсчитать
количество всех возможных треугольников в самом большом (на уровне n).
Вход. Первая строка содержит
количество тестов t (t ≤ 10000). Каждая строка содержит
одно целое число n (1 ≤ n ≤ 106) – уровень треугольника.
Выход. Для каждого теста вывести
в отдельной строке количество треугольников в наибольшем (на уровне n). Все ответы помещаются в
целочисленный 64-битовый тип.
|
Пример
входа |
Пример
выхода |
|
3 1 2 3 |
1 5 13 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Рассмотрим ряд
треугольников:
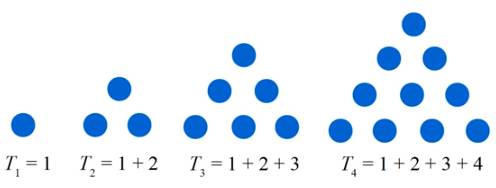
Обозначим через Tn количество точек в нем (назовем Tn треугольными
числами). По сумме
арифметической прогрессии Tn = n (n + 1) / 2.
Подсчитаем
сначала количество треугольников 
с вершиной вверх. Каждая
жирная точка на исходном треугольнике является вершиной некоторого меньшего
треугольника.
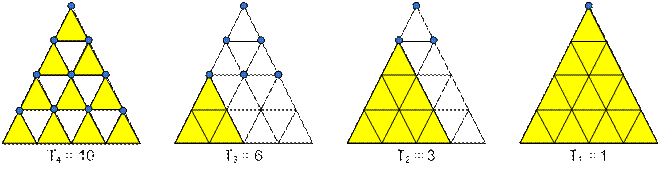
Количество треугольников со
стороной 1 равно Tn.
Количество треугольников со
стороной 2 равно Tn-1.
…
Количество треугольников со
стороной n равно T1.
Итого = Tn + Tn-1 + Tn-2 + … + T2 + T1 или = Tn + 
.
Теперь
подсчитаем количество треугольников 
с вершиной вниз.
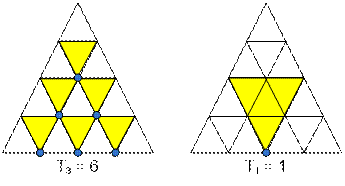
Количество треугольников со
стороной 1 равно Tn-1.
Количество треугольников со
стороной 2 равно Tn-3.
Количество треугольников со
стороной 3 равно Tn-5.
…
Количество треугольников со
стороной n равно 0.
Для четного n имеем: = Tn-1 + Tn-3 + … + T3 + T1.
Для нечетного n имеем: = Tn-1 + Tn-3 + … + T4 + T2.
Или = Tn-1 + 
.
Реализация алгоритма
Объявим рабочий массив.
#define MAX 1000010
long long s[MAX][2];
Вычисление значения Tn = n (n + 1) / 2.
long long T(long long n)
{
return n * (n + 1) / 2;
}
Основная часть программы. Инициализируем и затем вычисляем значения
и .
s[1][0] = 1; s[2][0] = 3;
s[1][1] = 0; s[2][1] = 1;
for(i = 2; i < MAX; i++)
{
s[i][0] = s[i-1][0] + T(i);
s[i][1] = s[i-2][1] + T(i-1);
}
Читаем входные данные и выводим ответ.
scanf("%d",&tests);
while(tests--)
{
scanf("%lld",&n);
printf("%lld\n",s[n][0] + s[n][1]);
}