4725. Сумма квадратов
Задано
натуральное число n. Вычислите сумму:
12 + 22 + 32 + ... + n2.
Вход. Одно
натуральное число n (1 ≤ n ≤ 106).
Выход. Выведите значение указанной суммы.
|
Пример
входа |
Пример
выхода |
|
2 |
5 |
РЕШЕНИЕ
элементарная
задача – формула
Анализ алгоритма
Указанную сумму
можно вычислить с помощью цикла. Однако здесь мы также представим формулу.
Пусть f(n) = 12 + 22
+ 32 + ... + n2.
Рассмотрим сумму:
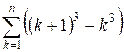= (n + 1)3 – 1 = n3 + 3n2 + 3n
Распишем сумму
следующим образом:
= 
= 
+ 
+ 
=
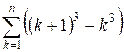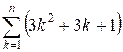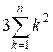= 3f(n) + 
+ n
Приравняем
правые части обоих равенств:
n3 + 3n2
+ 3n = 3 f(n) + 3 (n + 1) n / 2 + n,
n3 + 3 n2 / 2 + n / 2 = 3 f(n),
2 n3 + 3 n2 + n = 6 f(n),
f(n) = 
Реализация алгоритма
Реализуем
программу при помощи цикла.
scanf("%lld",&n);
for(i = 1; i <= n; i++)
sum += i * i;
printf("%lld\n",sum);
Реализация алгоритма – формула
Реализуем
программу при помощи формулы.
scanf("%lld",&n);
sum = n * (n +
1) * (2*n + 1) / 6;
printf("%lld\n",sum);
Java реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
long n = con.nextLong();
long sum = n * (n + 1) * (2 * n + 1) / 6;
System.out.println(sum);
con.close();
}
}
Python реализация – формула
Реализуем
программу при помощи формулы.
n = int(input())
sum = n * (n + 1) * (2*n + 1) // 6;
print(sum)
Python реализация – цикл
Реализуем
программу при помощи цикла.
n = int(input())
sum = 0
for i in range(1, n+1):
sum += i *
i;
print(sum)