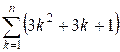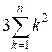4725. Sum of squares
Given the value of n.
Compute the following sum: 12 + 22 + 32 + ...
+ n2.
Input. One positive integer n.
Output. Print the value of the specified sum.
|
Sample
input |
Sample
output |
|
2 |
5 |
SOLUTION
elementary
problem – formula
Algorithm
analysis
The
specified sum
can be computed using a loop. However, we will also derive the formula. Let f(n) = 12 + 22 + 32
+ ... + n2. Consider the sum:
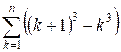 = (n + 1)3 – 1 = n3 + 3n2 + 3n
= (n + 1)3 – 1 = n3 + 3n2 + 3n
Expand the sum
as follows:
= 3f(n) + ![]() + n
+ n
Then, equate the
right-hand sides of both equations:
n3 + 3n2
+ 3n = 3 f(n) + 3 (n + 1) n / 2 + n,
n3 + 3 n2 / 2 + n / 2 = 3 f(n),
2 n3 + 3 n2 + n = 6 f(n),
f(n) = ![]()
Algorithm implementation
Implement the
program using a loop.
scanf("%lld",&n);
for(i = 1; i <= n; i++)
sum += i * i;
printf("%lld\n",sum);
Algorithm implementation– formula
Implement the
program using the formula.
scanf("%lld",&n);
sum = n * (n + 1) * (2*n + 1) / 6;
printf("%lld\n",sum);
Java implementation
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
long n = con.nextLong();
long sum = n * (n + 1) * (2 * n + 1) / 6;
System.out.println(sum);
con.close();
}
}
Python implementation–
formula
Implement the
program using the formula.
n = int(input())
sum = n * (n + 1) * (2*n + 1) // 6;
print(sum)
Python implementation–
loop
Implement the
program using a loop.
n = int(input())
sum = 0
for i in range(1, n+1):
sum += i * i;
print(sum)