4751. Diagonals

In the square table n × n find the sum of integers at the main and the secondary diagonals.

Input. The first line contains the size n (1 ≤ n ≤ 500) of the matrix. The next lines describe a matrix n × n. The elements of the matrix are not greater than 10⁵ by absolute value.

Output. Print the sum of the integers at the main and the secondary diagonals.

Sample input	Sample output
4 1 2 3 4 5 6 7 8 3 2 5 4 8 7 9 3	15 21

SOLUTION

array

Algorithm analysis

Let m be a two-dimensional array, where indexing starts from 0. Element m[i][j] lies on:

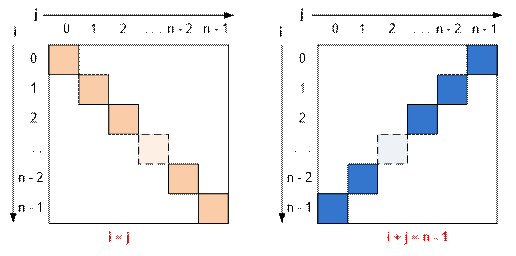
· the main diagonal if i = j;

· the secondary diagonal if i + j = n – 1;

Example

Consider the test case given.

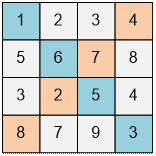
The sum of the integers at the main diagonal is 1 + 6 + 5 + 3 = 15.

The sum of the integers at the secondary diagonal is 8 + 2 + 7 + 4 = 21.

Algorithm realization

Read the input data. Read the elements of the matrix on the fly, without declaring a two-dimensional array.

scanf("%d",&n);

a = b = 0;

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

{

scanf("%d",&val);

Find the sum of the integers on the main diagonal in the variable a.

Find the sum of the integers on the secondary diagonal in the variable b.

if (i == j) a += val;

if (i + j == n - 1) b += val;

}

Print the answer.

printf("%d %d\n",a,b);

Algorithm realization – two-dimensional array

Declare a two-dimensional array.

int m[510][510];

Read the input data.

scanf("%d", &n);

for (i = 0; i < n; i++)

for (j = 0; j < n; j++)

scanf("%d", &m[i][j]);

Find the sum of the integers on the main diagonal in the variable a.

Find the sum of the integers on the secondary diagonal in the variable b.

a = b = 0;

Iterate over all elements of the two-dimensional array.

for (i = 0; i < n; i++)

for (j = 0; j < n; j++)

{

Element m[i][j] lies on the main diagonal if i = j;

if (i == j) a += m[i][j];

Element m[i][j] lies on the secondary diagonal if i + j = n – 1;

if (i + j == n - 1) b += m[i][j];

}

Print the answer.

printf("%d %d\n", a, b);

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m[][] = new int[n][n];

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

m[i][j] = con.nextInt();

int a = 0, b = 0;

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

{

if (i == j) a += m[i][j];

if (i + j == n - 1) b += m[i][j];

}

System.out.println(a + " " + b);

con.close();

}

}

Java realization – on fly

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int a = 0, b = 0;

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

{

int val = con.nextInt();

if (i == j) a += val;

if (i + j == n - 1) b += val;

}

System.out.println(a + " " + b);

con.close();

}

}

Python realization

n = int(input())

m = [[int(j) for j in input().split()] for i in range(n)]

a = b = 0

for i in range(n):

for j in range(n):

if i == j: a += m[i][j]

if i + j == n - 1: b += m[i][j]

print(a, b)