4819. Maximum by minimum
Directed unweighted graph is
given. Find in it a vertex, the shortest distance from which to the given one
is maximum, and print this distance.
Input.
First line contains three positive integers n,
m and s (1 ≤ s ≤ n ≤ 5000, 1 ≤ m ≤ 20000) – the number of
vertices and edges in the graph and the number of given vertex. In the next m lines the graph edges are given. Each
edge is given with the pair of numbers – the starting and the ending point.
Output. Print the required shortest distance.
|
Sample input 1 |
Sample output 1 |
|
3 5 3 1 2 2 1 3 1 2 3 3 3 |
2 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
5 4 5 1 2 2 3 3 4 4 5 |
4 |
SOLUTION
breadth first search
Algorithm analysis
Ñonstruct an
inverse directed graph – orient each edge in the opposite direction. Using
breadth-first search, find the shortest distances from the vertex s. The vertex v for which dist[v] is maximum will
be the desired one. In the problem you
must print the
value of dist[v].
Example
The graphs given
in the example have the following form (near the graph on the left given the inverted graph on
the right):
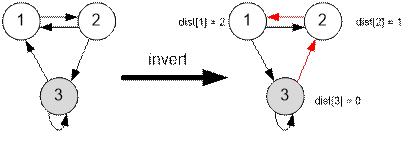
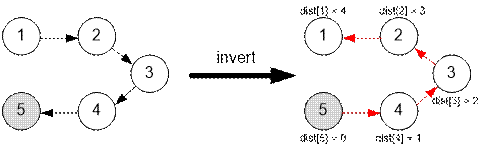
Algorithm realization
Declare
an adjacency matrix g and an array of shortest distances dist.
#define MAX 5001
int dist[MAX], g[MAX][MAX];
Breadth
first search from the vertex start.
void bfs(int start)
{
Initialize
the array of shortest distances.
memset(dist, -1, sizeof(dist));
dist[start] = 0;
Declare
the queue. Push to the
queue the starting vertex start.
queue<int> q;
q.push(start);
while (!q.empty())
{
int v = q.front(); q.pop();
for (int to = 1; to <= n; to++)
{
if (g[v][to] == 1 && dist[to] ==
-1)
{
q.push(to);
dist[to] = dist[v] + 1;
}
}
}
}
The main part of the program. Read the input
data.
scanf("%d %d %d", &n, &m, &s);
for (i = 0; i < m; i++)
{
scanf("%d %d", &u,
&v);
Construct a
graph. For each input directed edge u
→ v, put the inverse u → v into the graph.
g[v][u] = 1;
}
Start breadth first search
from the vertex s.
bfs(s);
Find the vertex i with
the maximum distance dist[i].
res = 0;
for (i = 1; i <= n; i++)
if (dist[i] >
res) res = dist[i];
Print the
required distance.
printf("%d\n", res);