4831. Knapsack
Find the maximum weight of gold that can be
carried in a knapsack with a capacity of s, if n gold bars are given with specified weights.
Input. The
first line contains one number s (1 ≤ s ≤ 104) – the knapsack capacity. Then given n (1 ≤ n
≤ 300) non-negative
integers, not exceeding 105
– the weights of bars.
Output. Print
the maximum weight of gold that can be carried in the knapsack.
|
Sample
input |
Sample
output |
|
20 5 7 12 18 |
19 |
SOLUTION
dynamic programming
Algorithm analysis
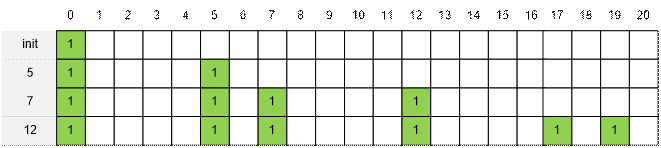
Create an array m, in which we set m[i] to 1, if we can obtain the weight i with the available ingots. Initially set m[0] = 1.
Let the array m have already been filled in the
required way for some set of bars. The next bar of weight w arrives. Then one should set to 1 all such m[i]
(w ≤ i ≤ s) for which m[i – w] = 1.
The answer is the largest weight, not bigger than s, that you can
carry in your knapsack.
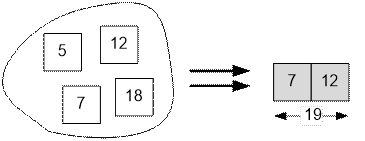
Example
For the given example, the maximum weight
of 19 is achieved for the subset {7, 12}.
Consider the filling of the cells of
array m with the arrival of the next bar. The weights of the bars are given on the left.
Algorithm realization
Declare the array.
#define MAX 10010
int m[MAX];
Read the input data.
scanf("%d",&s);
Initialization of array m.
memset(m,0,sizeof(m));
m[0] = 1;
Process the next
bar of weight w. Go through the
array m from right to left and set to 1 all such m[i]
(w ≤ i ≤ s) for which m[i
– w] = 1.
while(scanf("%d",&w)
== 1)
{
for(i = s; i >= w; i--)
if (m[i - w] == 1) m[i] = 1;
}
Look for the largest weight no more than s, that can be
carried in the knapsack, and print it.
for(i = s;; i--)
if (m[i] > 0) break;
printf("%d\n",i);
Algorithm realization – bitset
#include <cstdio>
#include <cstring>
#include <bitset>
#define MAX 10010
using namespace std;
bitset<MAX> m;
int i, s, w;
int main(void)
{
scanf("%d", &s);
m[0] = 1;
while (scanf("%d", &w) == 1)
{
for (i = s; i >= w;
i--)
if (m[i - w] == 1)
m[i] = 1;
}
for (i = s;; i--)
if (m[i] >
0) break;
printf("%d\n", i);
}