4853. Кратчайший путь
Задан неориентированный граф.
Найдите кратчайший путь от вершины a до вершины b.
Вход. В первой строке находится два целых числа n и m
(1 ≤ n ≤ 5 * 104,
1 ≤ m ≤ 105) –
количество вершин и рёбер соответственно.
Во второй строке заданы два целых числа a и b – начальная и конечная
вершины.
Далее следуют m строк, каждая из которых описывает одно ребро.
Выход. Если пути от a до b
не существует, выведите -1.
Иначе в первой строке
выведите длину l кратчайшего пути, а во второй строке выведите l
+ 1 число: последовательность вершин на этом пути.
|
Пример
входа |
Пример
выхода |
|
4 5 1 4 1 3 3 2 2 4 2 1 2 3 |
2 1 2 4 |
РЕШЕНИЕ
графы –
поиск в ширину
Анализ алгоритма
В задаче следует
реализовать поиск в ширину, построив массив кратчайших расстояний dist и
массив предков parent от истока до всех вершин. Поскольку количество
вершин порядка 50000, граф целесообразно хранить в виде списка смежности.
Пример
Приведенный в
примере граф имеет вид:
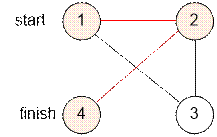
Реализация алгоритма
Объявим список
смежности g для хранения графа, а также дополнительные массивы:
·
dist[i] хранит
кратчайшее расстояние от истока до вершины i,
·
parent[i] хранит
предка вершины i при поиске в ширину.
vector<int> dist, parent;
vector<vector<int> > g;
Функция bfs реализует поиск в ширину из вершины start.
void bfs(int start)
{
// declare arrays
parent = vector<int>(n + 1, -1);
dist = vector<int>(n + 1, -1);
dist[start] = 0;
// initialize a queue
queue<int> q;
q.push(start);
while (!q.empty())
{
// remove vertex v from the queue
int v = q.front(); q.pop();
for (int to : g[v]) // there is an edge v
-> to
// if vertex v is not visited
if (dist[to] == -1)
{
q.push(to); // push to into the queue
dist[to] = dist[v] + 1; // recalculate the
shortest distance
parent[to] = v; // if v -> to, parent for to is v
}
}
}
Функция PrintPath выводит
кратчайший путь от истока до вершины v. Вершина v является начальной, если parent[v] = -1.
void PrintPath(int v)
{
if (v == -1) return;
PrintPath(parent[v]);
printf("%d ", v);
}
Основная часть
программы. Читаем входные данные.
scanf("%d %d", &n, &m);
scanf("%d %d", &a, &b);
Создаем список смежности графа.
g.resize(n + 1);
for (i = 0; i < m; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
Запускаем поиск в ширину из вершины a.
bfs(a);
Если при поиске вершина b не была достигнута (parent[b] = -1), выводим -1.
if (parent[b] == -1)
printf("-1\n");
else
{
В противном случае выводим длину кратчайшего пути до b
и сам путь.
printf("%d\n", dist[b]);
PrintPath(b);
}
Java реализация
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g;
static int dist[], parent[];
static int n, m;
static void bfs(int start)
{
Arrays.fill(dist,-1);
dist[start] = 0;
Arrays.fill(parent,-1);
Queue<Integer> q = new LinkedList<Integer>();
q.add(start);
while(!q.isEmpty())
{
int v = q.poll();
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (dist[to] == -1)
{
q.add(to);
dist[to] = dist[v] + 1;
parent[to] = v;
}
}
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt(); m = con.nextInt();
int a = con.nextInt();
int b = con.nextInt();
g = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
dist = new int[n+1];
parent = new int[n+1];
for (int i = 0; i < m; i++)
{
int u = con.nextInt();
int v = con.nextInt();
g[u].add(v);
g[v].add(u);
}
bfs(a);
if (parent[b] == -1)
System.out.println("-1");
else
{
System.out.println(dist[b]);
Vector<Integer> path = new
Vector<Integer>();
path.add(b);
while (parent[b] != -1)
{
b = parent[b];
path.add(b);
}
for (int i = path.size() - 1; i >= 0; i--)
System.out.print(path.get(i) + " ");
System.out.println();
}
con.close();
}
}