4861. Кружки в Маховниках

Маленький Петя очень любит компьютеры и хочет научиться программировать. В небольшом городке Маховники, где он живёт, работает сеть кружков по программированию самой разной тематики. Когда Петя пошел записываться, он увидел большой список, состоящий из n кружков. Петя хочет быть всесторонне развитой личностью, поэтому он собрался отучиться во всех этих кружках. Но когда он собрался записаться на все занятия сразу, обнаружилось, что не всё так просто. Вопервых, в один момент времени разрешается учиться только в одном из этих n кружков. Во-вторых, некоторые преподаватели выдвигают входные требования к знаниям учеников, заключающиеся в знании курсов каких-то других кружков!

Петя хочет стать великим программистом, поэтому подобные мелочи его не останавливают. Действительно, ему достаточно всего-лишь составить правильный порядок посещения кружков, чтобы удовлетворить всем входным требованиям - это совсем простая задача, доступная даже совсем неопытному программисту.

Перед тем как сесть составлять порядок посещения кружков, Петя внимательно перечитал условия обучения и обнаружил ещё один важный пункт. Оказывается, для привлечения школьников, во всех кружках действует система поощрения учеников конфетами. Это означает, что по окончании очередного кружка ученику выдают несколько коробок конфет, всё больше и больше с каждым пройденным кружком. С другой стороны, в каждом кружке количество конфет в коробке своё, зависящее от сложности курса. Более конкретно – за прохождение i-го по счёту кружка, если этот кружок идёт в общем списке под номером j, ученику выдают аж n^i-1 * j конфет – такие щедрые люди программисты. Петя решил совместить полезное с приятным – теперь он хочет выбрать такой порядок посещения кружков, чтобы при этом получить как можно больше конфет, однако эта задача ему уже не под силу. Помогите будущему великому человеку отыскать такой порядок.

Вход. В первой строке содержится целое число n (1 ≤ n ≤ 100 000) – количество кружков в Маховниках. В последующих n строках идут описания входных требований кружков, в порядке их следования в общем списке. В i-ой строке сначала записано целое число k_i (0 ≤ k_i ≤ n – 1) – количество кружков, в которых нужно отучиться перед записью в i-й кружок, а потом k_i номеров этих кружков. Сумма k_i не превосходит 200 000. Гарантируется, что возможно посетить все эти кружки в некотором порядке, не нарушая условия посещения.

Выход. Выведите n номеров, разделённых пробелами – порядок, в котором Пете надо посещать кружки, чтобы съесть как можно больше конфет.

Пример. Посещая кружки в указанном порядке, Петя получит 6⁰ * 2 + 6¹ * 1 + 6² * 3 + 6³ * 5 + 6⁴ * 4 + 6⁵ * 6 = 2 + 6 + 108 + 1080 + 5184 + 46656 = 53036 конфет.

Пример входа	Пример выхода
6 1 2 0 1 2 3 1 2 5 1 2 4 1 3 4 5	2 1 3 5 4 6

РЕШЕНИЕ

топологическая сортировка

Анализ алгоритма

Пусть (p₀, p₁, p₂, …, p_n-1) – порядок, в котором Петя будет посещать кружки. Тогда следует максимизировать значение

n⁰ * p₀ + n¹ * p₁ + n² * p₂ + … + n^n-1 * p_n-1

Поскольку n в задаче фиксировано, то указанное значение будет максимальным когда последовательность (p_n-1, … p₂, p₁, p₀) будет лексикографически наибольшей.

Построим обратный граф. Найдем для него лексикографически наибольшую топологическую сортировку и выведем ее в обратном порядке. Количество съеденных конфет для построенной последовательности будет максимальным.

Пример

Граф из условия задачи имеет вид:

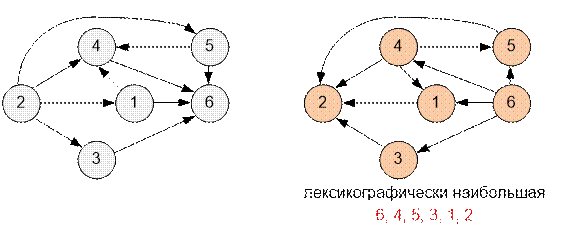
Для обратного графа лексикографически наибольшей топологической сортировкой будет (6, 4, 5, 3, 1, 2). Порядок посещения кружков будет обратный: (2, 1, 3, 5, 4, 6).

Реализация алгоритма

Объявим структуры данных. Входной граф содержится в списке смежности g. Входящие степени вершин храним в массиве InDegree. Топологическую сортировку строим в массиве Order. Множество maxHeap будет сортировать вершины по убыванию.

vector<vector<int> > graph;

vector<int> InDegree, Order;

set<int, greater<int> > maxHeap;

Читаем входные данные.

scanf("%d", &n);

graph.assign(n + 1, vector<int>());

InDegree.assign(n + 1, 0);

for (i = 1; i <= n; i++)

{

scanf("%d", &a);

for (j = 0; j < a; j++)

{

scanf("%d", &to);

Перед записью в i-ый кружок необходимо посетить кружок номер to. В исходном графе имеется ориентированнное ребро (to, i). Однако мы строим обратный граф. Следовательно для каждого ребра (i, to) увеличим InDegree[to] на 1.

graph[i].push_back(to);

InDegree[to]++;

}

}

Все вершины, входящие степени которых равны нулю, заносим во множество maxHeap.

for (i = 1; i < InDegree.size(); i++)

if (InDegree[i] == 0) maxHeap.insert(i);

Продолжаем работу алгоритма, пока множество maxHeap не пусто.

while (!maxHeap.empty())

{

Извлекаем вершину v из очереди с наибольшим номером. Заносим ее в топологический порядок Order.

v = *maxHeap.begin();

maxHeap.erase(maxHeap.begin());

Order.push_back(v);

Удаляем из графа ребра (v, to). Для каждого такого ребра уменьшаем входящую степень вершины to. Если степень вершины to станет нулевой, то заносим ее во множество maxHeap.

for (i = 0; i < graph[v].size(); i++)

{

to = graph[v][i];

InDegree[to]--;

if (InDegree[to] == 0) maxHeap.insert(to);

}

}

Массив Order содержит наибольшую топологическую сортировку. Выводим ее в обратном порядке.

for (i = Order.size() - 1; i >= 0; i--)

printf("%d ", Order[i]);

printf("\n");