4861. Sections in Makhovniki
Little Peter loves computers
and wants to learn programming. In the small town of Makhovniki, where he
lives, there is a network of programming sections on a wide variety of
subjects. When Peter went to sign up, he saw a large list of n sections. Peter wants to be a
comprehensively developed person, so he was going to learn in all these
sections. But when he was going to sign up for all the classes at once, it
turned out that everything was not so simple. First of all, at one time it is allowed
to study only in one of these n sections.
Secondly, some teachers put forward input requirements for the knowledge of
students, consisting in the knowledge of the courses of some other sections!
Peter wants to become a
great programmer, so such trifles do not stop him. Indeed, all he needs is just
to make up the correct order for visiting sections, in order to meet all the
input requirements – this is a very simple task, accessible even to a very
inexperienced programmer.
Before sitting down to make up
the order of visiting the sections, Peter carefully read the conditions of
study and found another important point. It turns out that in order to attract
schoolchildren, in all sections there is a system of encouraging pupils with
candies. This means that at the end of the next round, the student is given
several boxes of chocolates, more and more with each passing section. On the
other hand, in each section the number of candies in a box is different,
depending on the complexity of the course. More specifically – for passing the i-th section, if this section goes in
the general list with the number j,
the student is given as much ni-1 * j candies
– such generous people are programmers. Peter decided to combine the useful
with the pleasant – now he wants to choose such an order of visiting sections
so that to get as many candies as possible, however this task is no longer
within his power. Help the future great man find such an order.
Input.
The first line contains an integer n (1 ≤ n ≤ 100 000) – the number of sections in Makhovniki. The following n lines contain descriptions of the
input requirements for the sections, in the order in which they appear in the
general list. The i-th line first
contains an integer ki (0 ≤ ki ≤ n – 1) – the number
of sections where you need to learn before signing up to the i-th section, and then ki numbers of these
sections. The sum ki does
not exceed 200 000. It is guaranteed that it is possible to visit all
these sections in a certain order, without violating the conditions of the
visit.
Output. Print n space separated
numbers – the order in which Peter needs to attend the sections in order to eat
as many candies as possible.
Example. By visiting the sections in the specified order, Peter will receive 60 * 2 + 61 * 1 + 62 * 3 + 63 * 5 + 64 * 4 + 65 * 6 = 2 + 6 + 108 + 1080 + 5184 + 46656 = 53036 candies.
|
Sample input |
Sample output |
|
6 1 2 0 1 2 3 1 2 5 1 2 4 1 3 4 5 |
2 1 3 5 4 6 |
SOLUTION
topological sort
Algorithm analysis
Let (p0, p1, p2, …, pn-1) be the order in which Petya will visit the sections. Then
you should maximize the value
n0 * p0 + n1 * p1 + n2 * p2 + … + nn-1 * pn-1
Since n is fixed in the problem, the specified
value will be maximum when the sequence (pn-1, … p2, p1, p0) is
lexicographically the largest.
Construct a reverse
graph. Find the
lexicographically largest topological sort in it and print it in reverse order. The number of candies eaten for the
constructed sequence will be the maximum.
Example
The graph from
the statement has the
form
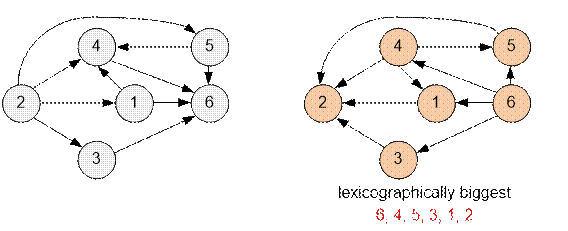
For the reverse graph, the
lexicographically largest topological sort is (6, 4, 5, 3, 1, 2). The order of
attending the sections will be
in the reverse order: (2, 1, 3, 5, 4,
6).
Algorithm realization
Let’s declare the data structures. Store the input graph in the adjacency list g. Store the incoming
degrees of the vertices in the array InDegree. Construct a topological sort
in the array Order. The set maxHeap will sort
the vertices in descending order.
vector<vector<int> > graph;
vector<int> InDegree, Order;
set<int, greater<int> > maxHeap;
Read the
input data.
scanf("%d", &n);
graph.assign(n + 1, vector<int>());
InDegree.assign(n + 1, 0);
for (i = 1; i <= n; i++)
{
scanf("%d", &a);
for (j = 0; j < a; j++)
{
scanf("%d", &to);
Before enrolling in the i-th section, you must
visit the section number to. The original graph has a
directed edge (to, i). However, we construct a reverse graph. Therefore, for each edge (i, to) we increase InDegree[to]
by 1.
graph[i].push_back(to);
InDegree[to]++;
}
}
All
vertices, which incoming degrees equals to zero, are inserted into the set maxHeap.
for (i = 1; i < InDegree.size(); i++)
if (InDegree[i] == 0) maxHeap.insert(i);
Continue
the algorithm until the set maxHeap
is empty.
while (!maxHeap.empty())
{
Extract the
vertex v from the queue with the
highest number. Put it into the topological order Order.
v = *maxHeap.begin();
maxHeap.erase(maxHeap.begin());
Order.push_back(v);
Delete the edges (v, to)
from the graph. For each such edge, we decrease the input degree of the vertex to. If the degree of the vertex to becomes
zero, insert it into the
set maxHeap.
for (i = 0; i <
graph[v].size(); i++)
{
to = graph[v][i];
InDegree[to]--;
if (InDegree[to] == 0) maxHeap.insert(to);
}
}
The array Order
contains the largest topological sort. Print it in the reverse order.
for (i = Order.size() - 1; i >= 0; i--)
printf("%d
", Order[i]);
printf("\n");