401. Письмо Шарика из Простоквашино
“Дорогой
дядя Федор!
Не слушай этого
старого ворчливого кота. Он еще не знает, какой я ему приготовил сюрприз,
поэтому можете загодя писать для него программу. Я ему количество квадратиков
со скобками увеличил до 300, количество заданий на день до 20, и усложнил само
задание.
Теперь ему нужно
искать количество вложений правильных скобочных последствий. Что это такое, я
прочел в одной умной книжке, которую потерял почтальон Печкин. Там написано
следующее:
“Пусть X – множество
правильно построенных скобочных выражений. Длиной правильно построенного
скобочного выражения E называется число одиночных скобок в E. Вложенность D(E)
множества E определяется следующим образом:
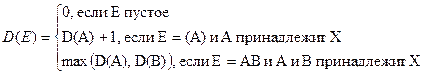
Например, длина
( )(( ))( ) равна 8, а вложенность 2.”
Понимая, что кот
все-таки не человек, я ему даю такие задания, где вложенность не менее 1 и не
более 200, а квадратиков со скобками выдаю не менее двух. Вот теперь он пусть поищет количество способов получить
правильные скобочные последовательности заданных длины и вложенности.
Так что спеши
выслать ему свою новую программу, ибо дою корову и молоко пью только я, пока
Матроскин занят вычислениями. Фотографию задумчивого Матроскина прилагаю.
Твой
верный друг и товарищ – Шарик”
Вход. Каждая строка содержит два числа n и d,
где n – количество выданных
квадратиков со скобками, а d –
глубина вложенности. Входные данные могут содержать пустые строки, которые
должны игнорироваться.
Выход. Для
каждого теста вывести в отдельной строке количество способов, которыми можно
получить правильно построенное скобочное выражение длины n и глубины d.
|
Пример входа |
Пример выхода |
|
6 2 300 150 |
3 1 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Любое непустое
скобочное выражение A длины n и глубины
не больше d можно представить в виде
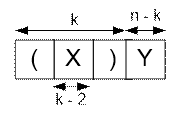
(X)Y, где X и Y – некоторые выражения, возможно пустые. Пусть длина выражения
(X) равна k. Тогда длина выражения X
равна k – 2, а длина Y равна n – k.
Очевидно, что 2 ≤ k ≤ n и k
может принимать только четные значения. При k
= 2 выражение X будет
пустым, а при k = n выражение
Y будет пустым. Отметим
также, что поскольку глубина выражения A не больше d, то глубина X не больше d
– 1, а глубина Y не больше d.
Обозначим через f(n,
d) количество способов, которыми
можно получить правильно построенное скобочное выражение длины n и глубины не больше d. Тогда имеется f(k – 2, d – 1) вариантов представления выражения
X и f(n – k, d) вариантов представления выражения Y.
Применяя правило умножения, можно утверждать, что при фиксированном k выражение (X)Y можно представить f(k
– 2, d – 1) * f(n – k, d)
вариантами. Таким образом
f(n, d)
= 
Поскольку в
задаче требуется найти количество способов, которыми можно получить правильно
построенное скобочное выражение длины n
и глубины в точности d, то ответом
будет значение g(n, d)
= f(n, d)
– f(n, d – 1).
Отдельно
необходимо обработать следующие случаи:
·
Если d
> n / 2, то g(n, d) = 0;
·
Если d
= n / 2, то имеем единственное
скобочное выражение (((…))) и g(n, n / 2) = 1;
·
Если d
= 1, то имеем единственное скобочное выражение ()()…()() и g(n, 1) = 1;
Пример
f(2, 2) = 
= f(0,
1) * f(0, 2) = 1* 1 = 1. Если
скобочное выражение длины 2 глубины не больше 2 представить в виде (X)Y, то
множителю f(0, 1) соответствует количество способов представить X, а множителю f(0, 2)
количество способов представить Y. Указанные множители равны единице, а X и Y соответствует
пустое выражение. То есть f(2, 2) соответствует единственное выражение ().
f(4, 2) = 
=
= f(0,
1) * f(2, 2) + f(2, 1) * f(0, 2) = 1 * 1
+ 1 * 1 = 2
Слагаемое f(0, 1) * f(2, 2) соответствует
выражению ()(), а f(2, 1) * f(0, 2) соответствует (()).
f(6, 2) = 
=
= f(0,
1) * f(4, 2) + f(2, 1) * f(2, 2) + f(4, 1) * f(0, 2) = 1 * 2 + 1 * 1 + 1 * 1 = 4
|
Слагаемое |
Соответствующие скобочные записи |
|
f(0, 1) * f(4, 2) |
()()(), ()(()) |
|
f(2, 1) * f(2, 2) |
(())() |
|
f(4, 1) * f(0, 2) |
(()()) |
Количество
правильно построенных скобочных выражений длины 6 и глубины в точности 2 равно
g(6, 2) = f(6,
2) – f(6, 1) = 4 – 1 = 3
Ими будут: ()(()),(())(),(()()).
Реализация
алгоритма
Значения f(n, d)
будем хранить в массиве длинных чисел ff.
BigInteger ff[301][151];
Функция f вычисляет значение f(n, d).
Отдельно обрабатываем случаи, когда n
< 0 или d < 0 (тогда функция
возвращает 0). Если n = 0, то f(0, d) считаем равным 1 при любом d (это случай, когда либо X, либо Y пустое).
BigInteger f(long long n, long long d)
{
long long k;
BigInteger &s = ff[n][d];
if ((n <
0) || (d < 0)) return 0;
if (!n) return ff[n][d] = BigInteger(1);
if (ff[n][d]
>= 0) return ff[n][d];
for(s = 0, k
= 2; k <= n; k += 2)
s = s + f(k - 2,d - 1) * f(n - k,d);
return s;
}
Основная часть
программы. Сначала отдельно обрабатываем частные случаи.
memset(ff,-1,sizeof(ff));
while(scanf("%lld
%lld",&n,&d) == 2)
{
if (d > n
/ 2) res = BigInteger(0); else
if ((d == n
/ 2) || (d == 1)) res = BigInteger(1); else
res = f(n,d) - f(n,d-1);
res.print();printf("\n");
}
Java реализация
import java.util.*;
import java.math.*;
public class Main
{
static BigInteger dp[][];
static BigInteger f(int n, int d)
{
BigInteger s = BigInteger.ZERO;
if ((n < 0) || (d < 0)) return BigInteger.ZERO;
if (n == 0) return dp[n][d] = BigInteger.ONE;
if (dp[n][d].compareTo(BigInteger.ZERO) >= 0) return dp[n][d];
for(int k = 2; k <= n; k += 2)
s = s.add(f(k - 2,d - 1).multiply(f(n - k,d)));
return dp[n][d] = s;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
while(con.hasNextInt())
{
int n = con.nextInt();
int d = con.nextInt();
dp = new BigInteger[n+1][d+1];
for(int i = 0; i <= n; i++)
for(int j = 0; j <= d; j++)
dp[i][j] = new BigInteger("-1");
BigInteger res = new BigInteger("0");
if (d > n / 2) res = BigInteger.ZERO; else
if ((d == n / 2) || (d == 1))
res = BigInteger.ONE; else
res = f(n,d).subtract(f(n,d-1));
System.out.println(res);
}
con.close();
}
}