468. Дерево
Одной из широко
известных структур данных для представления множеств является двоичное дерево
поиска. Каждый узел v такого дерева
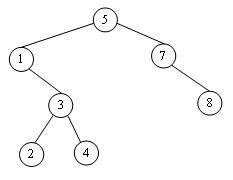
содержит один элемент множества, при этом все элементы в левом поддереве v должны быть меньше элемента в v, а элементы в правом поддереве v должны быть больше элемента в v. Пример двоичного дерева поиска
показан на рисунке. Узел называется корнем, если у него нет родителя (узел 5 на
рисунке). Узел называется листом, если у него нет детей (узлы 2, 4 и 8 на
рисунке). Путём в дереве назовём последовательность номеров узлов, таких что
каждый следующий узел является непосредственным потомком предыдущего.
Вам дана
последовательность неповторяющихся целых чисел. Требуется определить,
существует ли такое двоичное дерево поиска, в котором эта последовательность
является путём от корня к какому-то листу. Например, дерево поиска с путём
5-1-3-2 существует, а с путём 5-2-3-1 нет.
Вход. Задано последовательность чисел, разделённых пробелами
и/или переводами строк. До первого и после последнего числа могут быть пробелы
и переводы строк. Все числа различны. Количество чисел от 1 до 50 000. Значения
чисел от -2 147 483 648 до 2 147 483 647 включительно.
Выход. Выведите слово
"YES", если дерево, соответствующее заданному пути, существует, и
"NO" в противном случае.
|
Пример
входа |
Пример
выхода |
|
5 1 3 2 |
YES |
РЕШЕНИЕ
структуры
данных - дерево
Анализ алгоритма
Изначально
считаем, что все входное множество чисел лежит в промежутке [min; max]
= [-2 147 483 648; 2 147 483 647]. Рассмотрим два последовательных числа
входной последовательности: prev и cur. Если cur > prev, то далее
числа должны лежать в интервале [prev;
max]. Иначе следующие числа должны
принадлежать интервалу [min; prev].
Если на какой-то
итерации значение cur не принадлежит
текущему интервалу [min; max], то такого пути в дереве не
существует.
Реализация алгоритма
Объявим границы
[min; max] входных чисел.
max = 2147483647; min = max + 1;
Читаем
числа prev и cur.
scanf("%d",&prev);
while(scanf("%d",&cur)
== 1)
{
Если значение cur не принадлежит интервалу [min;
max], то искомого пути в дереве не
существует.
if ((cur < min) || (cur > max))
{
puts("NO");
return 0;
}
Изменяем
границы интервала [min; max].
if (cur > prev) min = prev; else max = prev;
prev = cur;
}
Если все
числа обработаны корректно, то искомый путь в дереве существует.
puts("YES");