482. Tri Tiling

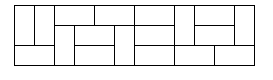
In how many ways can you tile a 3 * n rectangle with 2 * 1 dominoes? Here is a sample tiling of a 3 * 12 rectangle.

Input. Consists of several test cases followed by a line containing -1. Each test case is a line containing an integer n (0 ≤ n ≤ 30).

Output. For each test case print one integer giving the number of possible tilings.

Sample input	Sample output
2 8 12 -1	3 153 2131

SOLUTION

dynamic programming - combinatorics

Algorithm analysis

Denote by U_n the total number of tilings of a 3 * n rectangle with horizontal and vertical dominoes. Let V_n denote the total number of tilings of a 3 * n rectangle without a lower left corner with (3n – 1) / 2 dominoes.

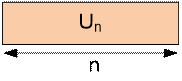
We get the following recurrence relations:

U_n = 2V_n-1 + U_n-2

V_n = U_n-1 + V_n-2

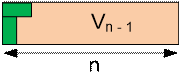
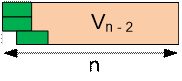
Consider the cases for n = 1 and n = 2.

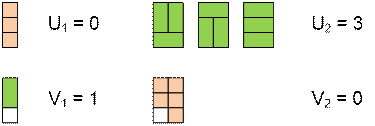
The recurrence relations can be used not only to calculate the values of functions forward, but also backward. By problem statement 0 ≤ n ≤ 30, so we need also the values U₀ and V₀. From derived relation we obtain

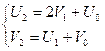or ,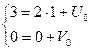

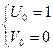
Example

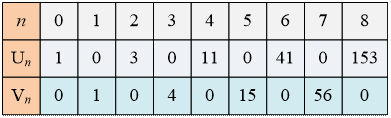
The values of U_n and V_n for small n we give in the table below:

Algorithm realization

In arrays u and v we shall compute the values of U_n and V_n.

int u[31], v[31];

Compute the values of U_n and V_n (n = 0, 1, …, 30) according to the above recurrence formulas.

u[0] = v[1] = 1;

u[1] = v[0] = 0;

for(n = 2; n <= 30; n++)

{

u[n] = 2 * v[n-1] + u[n-2];

v[n] = u[n-1] + v[n-2];

}

For each input number n print u[n].

while(scanf("%d",&n),n >= 0)

printf("%d\n",u[n]);

Java realization

import java.util.*;

public class Main

{

public static int MAX = 31;

static int u[] = new int[MAX];

static int v[] = new int[MAX];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

u[0] = v[1] = 1;

u[1] = v[0] = 0;

for(int n = 2; n < MAX; n++)

{

u[n] = 2 * v[n-1] + u[n-2];

v[n] = u[n-1] + v[n-2];

}

int n = con.nextInt();

while(n >= 0)

{

System.out.println(u[n]);

n = con.nextInt();

}

}

}