4973. Mutation

Genetic scientists from the planet Olympia are once again conducting experiments with the DNA of primitive organisms. The genome of an organism is a sequence of genes, each of which can be encoded by a natural number. Genes encoded by the same number are considered identical, while genes encoded by different numbers are considered different.

The scientists have already created a primitive organism and want to modify its genome in such a way as to produce an ideal organism. They believe that this will help develop cures for many diseases in the future.

An organism is considered ideal if any two identical genes are either located on adjacent positions in the genome or have at least one identical gene between them.

In one operation, scientists can select one or more identical genes in the genome, remove them, and then place them back into the genome, possibly at different positions. Since each such operation weakens the organism, the scientists aim to minimize the number of operations needed to achieve their goal.

Write a program that, given a representation of the genome, determines the minimum number of operations required to create an ideal organism.

Input. The first line contains the number of genes n (1 ≤ n ≤ 10⁵) in the genome of a primitive organism. The second line contains n positive integers, each of which does not exceed n – the sequence of genes in the genome.

Output. Print the minimum number of operations required to create an ideal organism.

Sample input	Sample output
9 1 2 1 3 1 3 2 4 5	2

SOLUTION

greedy

Algorithm analysis

The gene rearrangement should be performed in such a way that identical genes are placed next to each other. At the same time, it is necessary to minimize the number of operations performed.

For each positive integer a_i, we associate an interval [s_i; e_i], where s_i is the position where a_i first appears, and e_i is the position where a_i appears for the last time.

Let res be the maximum possible number of non-overlapping intervals. This value can be found using the “activity-selection” algorithm, which means that each of the remaining intervals overlaps with at least one of the selected intervals. After this, the described procedure should be applied to the genes corresponding to these intervals.

If k is the total number of constructed intervals, then the answer to the problem will be k – res.

Example

For the given example, the intervals will look like this (position numbering starts from zero):

· for 1: [0; 4];

· for 2: [1; 6];

· for 3: [3; 5];

· for 4: [7; 7];

· for 5: [8; 8];

Let’s sort the intervals by their end coordinate:

[0; 4], [3; 5], [1; 6], [7; 7], [8; 8]

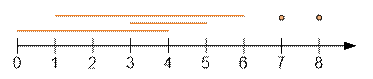
The maximum number of non-overlapping intervals is 3. For example, we can select the intervals [0; 4], [7; 7], [8; 8]. For the genes corresponding to the remaining intervals, the procedure described in the problem statement should be applied. The corresponding genes are 2 and 3. Two rearrangements can be performed, for example, as follows:

Algorithm implementation

Let MAX be the maximum possible number of genomes in the input sequence.

#define MAX 100001

The vector of pairs v stores the segments [s_i; e_i].

vector<pair<int, int> > v;

int s[MAX], e[MAX];

Read the input data. Initialize s[i] = -1, e[i] = -1.

scanf("%d", &n);

memset(s, -1, sizeof(s));

memset(e, -1, sizeof(e));

for (i = 0; i < n; i++)

{

scanf("%d", &x);

If the number x appears for the first time, record its position in the input sequence in s[x].

if (s[x] == -1) s[x] = i;

If the number x does not appear for the first time, record its position in e[x], assuming that x appears for the last time.

if (i > e[x]) e[x] = i;

}

All the constructed intervals are stored in the vector v.

for (i = 1; i <= n; i++) // numbers 1..n

if (s[i] != -1) v.push_back(make_pair(e[i], s[i]));

The intervals are stored in the vector in reverse order (in the form [e_i; s_i]) so that, by default, the intervals are sorted in ascending order of their ends.

sort(v.begin(), v.end());

Find the maximum number res of non-overlapping intervals.

i = res = 0;

while (i < v.size())

{

Add the i-th interval to the set of non-overlapping intervals. The variable temp holds the end of this interval (let’s call it the current interval).

res++; temp = v[i++].first; // end

As long as the start of the next interval is less than the end of the current interval, skip such an interval, as it overlaps with the current one.

while (i < v.size() && v[i].second < temp) i++;

}

Print the answer.

printf("%d\n", v.size() - res);