5071. Рой и копилки

 

У Роя есть n копилок пронумерованных от 1 до n. Каждый день он выбирает два индекса [l, r] и добавляет 1 монетку во все копилки начиная с l и до r (обе включительно). Он совершает такую операцию m дней.

После m дней у Роя возник вопрос: сколько копилок содержат как минимум x монет. У него q таких вопросов.

 

Вход. Первая строка содержит количество копилок n (1 ≤ n ≤ 106). Вторая строка содержит количество дней m (1 ≤ m ≤ 106). Каждая из следующих m строк содержит два целых числа l и r (1 ≤ l ≤ r ≤ n). Далее следует количество запросов q (1 ≤ q ≤ 106). Каждая из следующих q строк содержит одно целое число x (1 ≤ x ≤ n).

 

Выход. Для каждого запроса выведите ответ в отдельной строке.

 

Пример входа

Пример выхода

7

4

1 3

2 5

1 2

5 6

4

1

7

4

2

6

0

0

4

 

 

РЕШЕНИЕ

структуры данных

 

Анализ алгоритма

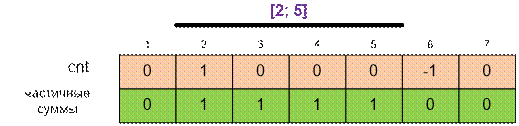
Заведем массив – счетчик cnt. Для каждого запроса [l, r] выполним две операции: cnt[l]++ и cnt[r + 1]--. Таким образом, частичная сумма 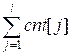 будет равна количеству монет в i-ой копилке.

Количество дней, в которые Рой совершает действия, не превышает 106. Каждый день он кладет в каждую копилку не более одной монеты. После выполнения всех действий в каждой копилке будет находиться не более 106 монет. Заведем массив coins размера 106 и занесем в coins[i] количество копилок с суммой i. Для этого для каждой частичной суммы sum = 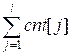 положим coins[sum]++.

Вычислим количество копилок, которые содержат как минимум x монет. Для этого в массиве coins пересчитаем его частичные суммы справа налево (то есть с конца). Тогда количество копилок, которые содержат как минимум x монет, будет равно coins[x].

 

Пример

 

 

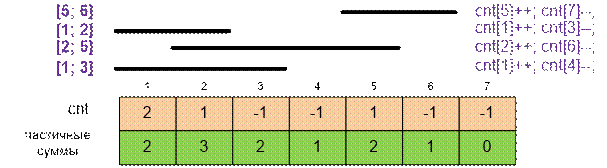
Получим следующее распределение монет по копилкам:

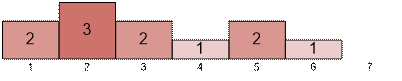
Количество копилок с суммой s. Частичные суммы (подсчитанные справа налево) содержат количество копилок, содержащих как минимум s монет.

 

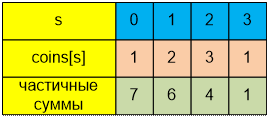
Имеются одна копилка с суммой 0 (копилка номер 7), две копилки с суммой 1 (копилки номер 4 и 6), три копилки с суммой 2 (копилки номер 1, 3 и 5), одна копилка с суммой 3 (копилка номер 2).

Вычислив частичные суммы массива coins, можно утверждать, например, что существует 6 копилок, содержащих как минимум 1 монету. Или что существует 4 копилки, содержащих как минимум 2 монеты.

 

Реализация алгоритма

Объявим рабочие массивы.

 

#define MAX 1000010

int cnt[MAX], coins[MAX];

 

Читаем входные данные. Строим массив cnt.

 

scanf("%d %d",&n,&m);

for(i = 0; i < m; i++)

{

  scanf("%d %d",&l,&r);

  cnt[l]++; cnt[r+1]--;

}

 

В переменной sum подсчитываем частичные суммы массива cnt. i-ая частичная сумма равна количеству монет в i-ой копилке. coins[i] равно количеству копилок с суммой i.

 

sum = 0;

for(i = 1; i <= n; i++)

{

  sum += cnt[i];

  coins[sum]++;

}

 

В массиве coins пересчитаем его частичные суммы справа налево.

 

for(i = MAX - 2; i >= 0; i--)

  coins[i] += coins[i+1];

 

Читаем количество запросов q. Для каждого запроса читаем значение x и выводим ответ coins[x].

 

scanf("%d",&q);

for(i = 0; i < q; i++)

{

  scanf("%d",&x);

  printf("%d\n",coins[x]);

}

 

Python реализация

Объявим рабочие списки.

 

MAX = 1000010

cnt = [0] * MAX

coins = [0] * MAX

 

Читаем входные данные.

 

n = int(input())

m = int(input())

 

Строим список cnt.

 

for _ in range(m):

  l, r = map(int, input().split())

  cnt[l] += 1

  cnt[r + 1] -= 1

 

В переменной sum подсчитываем частичные суммы списка cnt. i-ая частичная сумма равна количеству монет в i-ой копилке. coins[i] равно количеству копилок с суммой i.

 

sum = 0

for i in range(1, n + 1):

  sum += cnt[i]

  coins[sum] += 1

 

В массиве coins пересчитаем его частичные суммы справа налево.

 

for i in range(MAX - 2, -1, -1):

  coins[i] += coins[i + 1]

 

Читаем количество запросов q. Для каждого запроса читаем значение x и выводим ответ coins[x].

 

q = int(input())

for _ in range(q):

  x = int(input())

  print(coins[x])