5071. Roy and Coin Boxes

 

Roy has n coin boxes numbered from 1 to n. Every day he selects two indices [l, r] and adds 1 coin to each coin box starting from l to r (both inclusive). He does this for m number of days.

After m days, Roy has a query: how many coin boxes have at least x coins. He has q such queries.

 

Input. First line contains number of coin boxes n (1 ≤ n ≤ 106). Second line contains number of days m (1 ≤ m ≤ 106). Each of the next m lines consists of two space separated integers l and r (1 ≤ l ≤ r ≤ n). Followed number is the number of queries q (1 ≤ q ≤ 106). Each of next q lines contain a single integer x (1 ≤ x ≤ n).

 

Output. For each query output the result in a new line.

 

Sample input

Sample output

7

4

1 3

2 5

1 2

5 6

4

1

7

4

2

6

0

0

4

 

 

SOLUTION

data structures

 

Algorithm analysis

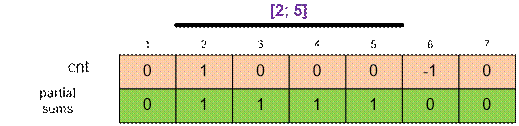
Let’s create an array cnt as a counter. For each query [l, r], we’ll perform two operations: cnt[l]++ and cnt[r + 1]--. Thus, the partial sum 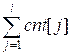 will equal the number of coins in the i-th coin box.

 

The number of days Roy performs actions is no more than 106. Each day he puts no more than one coin in each coin box. After completing all the actions, each coin box will contain no more than 106 coins. Create an array coins of size 106 and assign to coins[i] the number of coin boxes with i coins. To do this, for each partial sum sum = 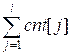 execute coins[sum]++.

Now let’s find the number of coin boxes that contain at least x coins. To do this, compute the partial sums in the coins array from right to left (that is, from the end). Then the number of coin boxes that contain at least x coins equals coins[x].

 

Example

 

 

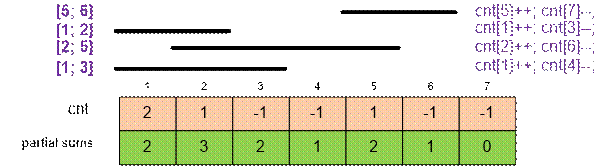
We get the following distribution of coins by coin boxes:

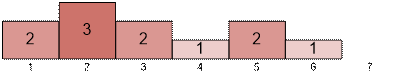
The number of coin boxes with a sum of s. Partial sums (counted from right to left) indicate the number of coin boxes with at least s coins.

 

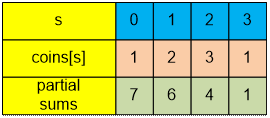
There is one coin box with a sum of 0 (coin box number 7), two coin boxes with a sum of 1 (coin boxes numbered 4 and 6), three coin boxes with a sum of 2 (coin boxes numbered 1, 3 and 5), and one coin box with a sum of 3 (coin box number 2).

After computing the partial sums of the coins array, it can be stated, for example, that there are 6 coin boxes containing at least 1 coin or that there are 4 coin boxes containing at least 2 coins.

 

Algorithm realization

Declare the arrays.

 

#define MAX 1000010

int cnt[MAX], coins[MAX];

 

Read the input data. Construct the array cnt.

 

scanf("%d %d",&n,&m);

for(i = 0; i < m; i++)

{

  scanf("%d %d",&l,&r);

  cnt[l]++; cnt[r+1]--;

}

 

Compute the partial sums of the cnt array in the variable sum. The i-th partial sum equals the number of coins in the i-th coin box. coins[i] equals the number of coin boxes with a sum of i.

 

sum = 0;

for(i = 1; i <= n; i++)

{

  sum += cnt[i];

  coins[sum]++;

}

 

Recompute the partial sums in the coins array from right to left.

 

for(i = MAX - 2; i >= 0; i--)

  coins[i] += coins[i+1];

 

Read the number of queries q. For each query, read the value x and print the answer coins[x].

 

scanf("%d",&q);

for(i = 0; i < q; i++)

{

  scanf("%d",&x);

  printf("%d\n",coins[x]);

}

 

Python realization

Declare the lists.

 

MAX = 1000010

cnt = [0] * MAX

coins = [0] * MAX

 

Read the input data.

 

n = int(input())

m = int(input())

 

Construct the list cnt.

 

for _ in range(m):

  l, r = map(int, input().split())

  cnt[l] += 1

  cnt[r + 1] -= 1

 

Compute the partial sums of the cnt list in the variable sum. The i-th partial sum equals the number of coins in the i-th coin box. coins[i] equals the number of coin boxes with a sum of i.

 

sum = 0

for i in range(1, n + 1):

  sum += cnt[i]

  coins[sum] += 1

 

Recompute the partial sums in the coins list from right to left.

 

for i in range(MAX - 2, -1, -1):

  coins[i] += coins[i + 1]

 

Read the number of queries q. For each query, read the value x and print the answer coins[x].

 

q = int(input())

for _ in range(q):

  x = int(input())

  print(coins[x])