5074. Степени вершин по спискам ребер

Неориентированный граф задан списком ребер. Найдите степени всех вершин графа.

Вход. Первая строка содержит количество вершин в графе n (1 ≤ n ≤ 100) и количество ребер m (1 ≤ m ≤ n * (n – 1) / 2). Затем следуют m пар чисел – ребра графа.

Выход. Выведите n чисел – степени вершин графа.

Пример входа	Пример выхода
4 4 1 2 1 3 2 3 3 4	2 2 3 1

РЕШЕНИЕ

графы

Анализ алгоритма

Построим массив deg, где deg[i] содержит степень i-ой вершины.

Для каждого ребра (a, b) увеличим степень вершин a и b (deg[a]++, deg[b]++).

Пример

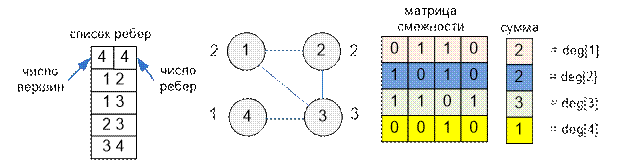
Граф, приведенный в примере, имеет вид:

Реализация алгоритма

Объявим массив deg, где deg[i] будет содержать степень i-ой вершины.

int deg[101];

Читаем количество вершин и ребер.

scanf("%d %d", &n, &m);

Для каждого ребра (a, b) увеличиваем степень вершин a и b.

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

deg[a]++; deg[b]++;

}

Выводим степени вершин.

for (i = 1; i <= n; i++)

printf("%d\n", deg[i]);