5076. Регулярный граф

Неориентированный граф называется регулярным, если все его вершины имеют одинаковую степень.

Для заданного списком ребер графа проверьте, является ли он регулярным.

Вход. Первая строка содержит число n (1 ≤ n ≤ 100) вершин и число m (m ≤ n (n – 1) / 2) ребер в графе. Затем следует m пар чисел – ребра графа.

Выход. Выведите YES если граф является регулярным и NO в противном случае.

Пример входа 1	Пример выхода 1
3 3 1 2 1 3 2 3	YES
Пример входа 2	Пример выхода 2
3 2 1 2 2 3	NO

РЕШЕНИЕ

графы

Анализ алгоритма

Вычислим степень каждой вершины графа. Если все степени вершин графа равны, то граф регулярный, иначе – нет.

Пример

Графы, приведенные в примерах, имеют вид:

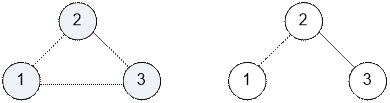
Степени всех вершин первого графа равны 2, поэтому граф регулярный. Во втором примере вершины графа имеют разную степень. Второй граф не регулярный.

Реализация алгоритма

Степени вершин подсчитываем в массиве deg.

#define MAX 110

int deg[MAX];

Читаем входные данные.

scanf("%d %d",&n,&m);

memset(deg,0,sizeof(deg));

for(i = 0; i < m; i++)

{

Для каждого неориентированного ребра (a, b) увеличиваем на 1 степени вершин a и b.

scanf("%d %d",&a,&b);

deg[a]++; deg[b]++;

}

Проверяем, одинаковы ли все значения массива deg. Если они все равны (степени всех вершин графа одинаковы), то flag = 0 и граф регулярный.

flag = 0;

for(i = 1; i < n; i++)

if (deg[i] != deg[i+1]) flag = 1;

В зависимости от значения переменной flag выводим ответ.

if (flag == 0) printf("YES\n");

else printf("NO\n");

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

int deg[] = new int[n+1];

for(int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

deg[a]++;

deg[b]++;

}

int flag = 0;

for(int i = 1; i < n; i++)

if (deg[i] != deg[i+1]) flag = 1;

if (flag == 0) System.out.println("YES");

else System.out.println("NO");

con.close();

}

}