5078. Граф турнир

Ориентированный граф называется турниром, если между любой парой его различных вершин существует ровно одно ребро. Для заданного списком ребер графа проверьте, является ли он турниром.

Вход. Первая строка содержит количество вершин n (1 ≤ n ≤ 100) и количество ребер m (1 ≤ m ≤ n * (n – 1) / 2) в графе. Затем следуют m пар чисел – ребра графа.

Выход. Выведите “YES” если граф является турниром и “NO” в противном случае.

Пример входа	Пример выхода
4 6 1 2 1 3 4 1 2 3 4 2 4 3	YES

РЕШЕНИЕ

графы

Анализ алгоритма

Пусть g[101][101] – двумерный массив. Для каждого ребра графа (i, j) увеличим значение g[i][j] на единицу. Граф является турниром, если после обработки всех его ребер для любых разных вершин i и j справедливо равенство:

g[i][j] + g[j][i] = 1

Пример

Граф, приведенный в примере, имеет вид:

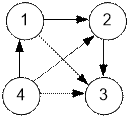
Реализация алгоритма

Объявим двумерный массив g.

#define MAX 101

int g[MAX][MAX];

Читаем входные данные. Для каждого ребра (a, b) увеличим значение g[a][b] на 1.

scanf("%d %d", &n, &m);

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a][b]++;

}

Граф является турниром, если g[i][j] + g[j][i] = 1 для любых разных вершин i и j. Проверим это свойство. Установим flag = 1 если граф является турниром и flag = 0 иначе.

flag = 1; // OK

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

if ((i != j) && (g[i][j] + g[j][i] != 1)) flag = 0;

В зависимости от значения переменной flag выводим результат.

if (flag == 1) puts("YES"); else puts("NO");