5084. Интервальный запрос меньше

Имеется массив целых чисел длины n. Вам следует ответить на q запросов: сколько чисел из интервала [l, r] имеют значение меньше x.

Вход. Первая строка содержит длину массива n (1 ≤ n ≤ 2 * 10⁵). Следующая строка содержит n чисел. В следующей строке задано количество q (1 ≤ q ≤ 10⁵) запросов. Каждая из следующих q строк содержит один запрос: три целых числа l, r и x (l ≤ r, 1 ≤ x ≤ 10⁹).

Выход. Для каждого запроса выведите в отдельной строке количество чисел из интервала [l, r], которые меньше x.

Пример входа	Пример выхода
8 1 3 2 4 3 10 5 5 4 1 8 5 1 4 3 5 8 9 2 6 4	5 2 3 3

РЕШЕНИЕ

структуры данных – дерево отрезков

Анализ алгоритма

Алгоритм Merge tree. Заведем в каждой вершине дерева отрезков дополнительный массив. Вершина, соответствующая фундаментальному отрезку [i; j], содержит в своем массиве отсортированный набор чисел a_i, …, a_j. Время построения такого дерева составляет O(nlog₂n).

Тогда для нахождения количества чисел из интервала [l, r], которые меньше x, следует разбить этот интервал на множество фундаментальных отрезков и в каждом из них совершить бинарный поиск, подсчитав количество элементов, меньших x. Время запроса составит .

Пример

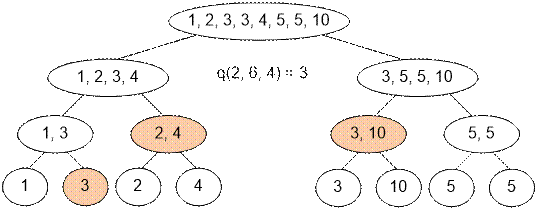
Реализация алгоритма

Объявим дерево отрезков. В каждой ее вершине храним массив чисел.

vector<vector<int> > SegTree;

Входные числа храним в массиве а.

vector<int> a;

Функция BuildTree строит дерево отрезков по массиву а. Отсортированный массив в каждой вершине получается в результате слияния массивов ее сыновей за O(n) при помощи команды merge.

void BuildTree(int v, int lpos, int rpos)

{

if (lpos == rpos)

SegTree[v].push_back(a[lpos]);

else

{

int mid = (lpos + rpos) / 2;

BuildTree(2*v, lpos, mid);

BuildTree(2*v+1, mid+1, rpos);

SegTree[v].resize(rpos - lpos + 1);

merge(SegTree[2*v].begin(), SegTree[2*v].end(),

SegTree[2*v+1].begin(), SegTree[2*v+1].end(),

SegTree[v].begin());

}

}

Функция Query подсчитывает количество чисел на интервале [l, r], которые меньше x. Для каждого фундаментального отрезка [left; right] при помощи функции lower_bound находим количество чисел, меньших x.

int Query(int v, int lpos, int rpos, int left, int right, int x)

{

if (left > right) return 0;

if ((lpos == left) && (rpos == right))

return lower_bound(SegTree[v].begin(), SegTree[v].end(), x) –

SegTree[v].begin();

int mid = (lpos + rpos) / 2;

return Query(2*v, lpos, mid, left, min(mid, right), x) +

Query(2*v+1, mid+1, rpos, max(left, mid+1), right, x);

}

Основная часть программы. Читаем входной массив чисел.

scanf("%d",&n);

a.resize(n + 1);

for(i = 1; i <= n; i++)

scanf("%d",&a[i]);

Строим по массиву а дерево отрезков.

SegTree.resize(4*n);

build(1,1,n);

Последовательно выполняем q запросов.

scanf("%d",&q);

for(i = 0; i < q; i++)

{

scanf("%d %d %d",&l,&r,&x);

printf("%d\n",Query(1,1,n,l,r,x));

}

Реализация алгоритма – SQRT декомпозиция

#include <cstdio>

#include <vector>

#include <set>

#include <algorithm>

#include <cmath>

using namespace std;

vector<int> a;

vector<vector<int> > b;

int i, n, q, len, blocks, l, r, x;

int main()

{

scanf("%d", &n);

a.resize(n);

len = sqrt(n) + 1;

blocks = ceil((double)n / len);

b.resize(len);

for (i = 0;i < n; i++)

{

scanf("%d", &a[i]);

b[i / len].push_back(a[i]);

}

scanf("%d", &q);

for (i = 0;i < blocks; i++)

sort(b[i].begin(), b[i].end());

while (q--)

{

scanf("%d %d %d", &l, &r, &x);

l--; r--;

int res = 0;

int c_l = l / len, c_r = r / len;

if (c_l == c_r)

{

for (i = l; i <= r; i++)

if (a[i] < x) res++;

}

else

{

for (i = l; i <= (c_l + 1)*len - 1; i++)

if (a[i] < x) res++;

for (i = c_l + 1; i <= c_r - 1; i++)

res += lower_bound(b[i].begin(), b[i].end(), x) - b[i].begin();

for (i = c_r * len; i <= r; i++)

if (a[i] < x) res++;

}

printf("%d\n", res);

}

return 0;

}