5091. Взрывоопасные
контейнеры
Все
контейнеры в мире делятся на две категории – с тротилом и без. Только глупец
поставит ящик с тротилом на другой ящик с тротилом. Поскольку вы явно не из
таких (правда?), вам прекрасно известно: тротил взрывается, особенно если на
нём оказывается ещё один ящик с тротилом.
Вы
находитесь в комнате, где в огромном количестве представлены оба типа ящиков.
Вдруг из люка появляется подъемник, который, к сожалению, неисправен. Он решил
построить башню из n ящиков. Чтобы оценить свои шансы на выживание, вам
нужно посчитать количество возможных вариантов, при которых ничего не
взорвётся.
Кстати,
задумайтесь: что здравомыслящий человек вроде Вас делает в комнате с горой
тротила?
Вход. Одно целое число n (1 ≤ n < 45).
Выход. Выведите количество безопасных
способов построить башню.
|
Пример
входа 1 |
Пример
выхода 1 |
|
1 |
2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
2 |
3 |
РЕШЕНИЕ
числа
Фибоначчи
Анализ алгоритма
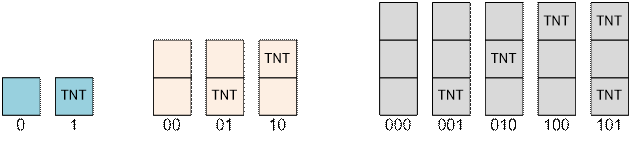
Каждый пустой
ящик обозначим 0, а ящик с тротилом 1. Задача состоит в том, чтобы найти
количество строк длины n, состоящих из 0 и 1, таких, что две единицы не
стоят рядом.
Ответом на
задачу будет число Фибоначчи f(n):
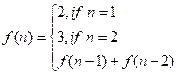
Пример
Рассмотрим всевозможные
башни высоты n = 1, n = 2, n = 3. Каждой из них
соответствует последовательность из 0 и 1.
·
две башни высоты 1: “0”, “1”;
·
три башни высоты 2: “00”, “01”, “10”;
·
пять башен высоты 3: “000”, “001”, “010”, “100”, “101”;
Реализация алгоритма
Объявим рабочий
массив.
#define MAX 45
int fib[MAX];
Заполним элементы массива fib числами Фибоначчи в соответствии с
рекуррентной формулой.
fib[1] = 2; fib[2] = 3;
for (int i = 3; i < MAX; i++)
fib[i] = fib[i - 1] + fib[i - 2];
Читаем входное значение n и выводим
ответ.
scanf("%d", &n);
printf("%d\n", fib[n]);
Реализация алгоритма –
мемоизация
Объявим рабочий
массив.
#define MAX 45
int fib[MAX];
Функция f вычисляет n-ое число
Фибоначчи.
int f(int n)
{
if (n == 1) return 2;
if (n == 2) return 3;
if (fib[n] != -1) return fib[n];
return fib[n] = f(n - 1) + f(n - 2);
}
Основная часть программы. Читаем входное значение n и выводим ответ.
scanf("%d", &n);
memset(fib, -1, sizeof(fib));
printf("%d\n", f(n));
Java реализация
import java.util.*;
public class Main
{
static int fib[] = new int[45];
static int f(int n)
{
if (n ==
1) return 2;
if (n ==
2) return 3;
if (fib[n] !=
-1) return fib[n];
return fib[n] = f(n-1) +
f(n - 2);
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
Arrays.fill(fib,
-1);
System.out.println(f(n));
con.close();
}
}
Python реализация – список
Заполним элементы списка lst числами
Фибоначчи в
соответствии с рекуррентной формулой.
lst = [0, 2, 3]
for i in range(3, 45):
lst.append(lst[i - 2] + lst[i - 1])
Читаем входное значение n и выводим ответ.
n = int(input())
print(lst[n])
Python реализация – запоминание
Функция fib вычисляет n-ое число
Фибоначчи.
def fib(n):
if dp[n] != -1:
return dp[n]
dp[n] = fib(n - 1) + fib(n - 2)
return dp[n]
Основная часть программы. Читаем входное
значение n.
n = int(input())
Список dp будет содержать числа
Фибоначчи. Инициализируем его начальные значения.
dp = (n + 2) * [-1]
dp[1] = 2
dp[2] = 3
Вычисляем и выводим ответ.
print(fib(n))