5092. Honeycomb

The bee can go in honeycomb as shown in the figure - with moves 1 and 2 from upper row and with move 3 from the lower.

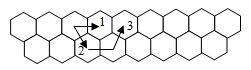
Input. The number of hexagons n (1 ≤ n ≤ 45) in the upper row. The lower row contains 1 hexagon less.

Output. Print the number of ways to get from the first cell of the top row to the last cell of the same row.

Sample input	Sample output
3	2

SOLUTION

dynamic programming – Fibonacci numbers

Algorithm analysis

Enumerate the honeycomb in the next way:

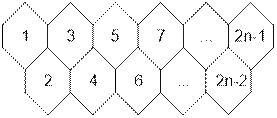
Let f(k) be the number of ways to get from the first honeycomb into the k-th one. If upper row contains n honeycomb, the number of rightmost honeycomb of upper row has number 2n – 1. So the answer to the problem will be f(2n – 1).

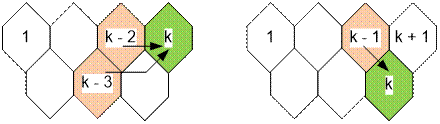
If k-th honeycomb is located in the upper row, the bee can come into it either from (k – 2)-th honeycomb, or from (k – 3)-th. So f(k) = f(k – 2) + f(k – 3) for odd k.

If k-th honeycomb is located in the lower row, the bee can come into it only from (k – 1)-th honeycomb. So f(k) = f(k – 1) for even k.

Calculate the base cases separately: f(1) = 1, f(2) = 1, f(3) = 1.

Algorithm realization

Declare fib array.

#define MAX 100

int fib[MAX];

Fill the cells of array fib according to recursive formula given above.

fib[0] = 0; fib[1] = 1; fib[2] = 1;

for(int i = 3; i < MAX; i++)

if (i % 2 == 1) fib[i] = fib[i-2] + fib[i-3];

else fib[i] = fib[i-1];

Read the value of n and print the answer f(2n – 1).

scanf("%d",&n);

printf("%d\n",fib[2*n-1]);

Algorithm realization – recursion + memorization

#include <stdio.h>

#include <string.h>

int n, fib[90];

int f(int n)

{

if (n == 1) return 1;

if (n == 2) return 1;

if (n == 3) return 1;

if (fib[n] != -1) return fib[n];

if (n % 2 == 1) return fib[n] = f(n - 2) + f(n - 3);

return fib[n] = f(n - 1);

}

int main(void)

{

scanf("%d",&n);

memset(fib,-1,sizeof(fib));

printf("%d\n",f(2*n-1));

return 0;

}

Java realization

import java.util.*;

public class Main

{

static int fib[] = new int[90];

static int f(int n)

{

if (n <= 3) return 1;

if (fib[n] != -1) return fib[n];

if (n % 2 == 1) return fib[n] = f(n - 1) + f(n - 3);

return fib[n] = f(n - 1);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

Arrays.fill(fib, -1);

System.out.println(f(2*n-1));

con.close();

}

}