5101. Ходжа Насреддин

Ходжа Насреддин находится в левой верхней клетке таблицы размером n × n, а его осел – в правой нижней. Ходжа может двигаться только вправо или вниз, а осел – только влево или вверх.

Сколькими способами они могут встретиться в одной клетке? Два способа считаются различными, если в них хотя бы один из маршрутов Ходжи или осла отличается от другого.

Вход. Одно число n (1 ≤ n ≤ 50).

Выход. Выведите одно число – количество способов, которыми Ходжа и осел могут встретиться. Поскольку это число может быть очень большим, выведите его по модулю 9929.

Пример входа	Пример выхода
3	30

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть a[i][j] содержит количество путей, которыми Ходжа Насреддин может добраться из клетки (1, 1) в клетку (i, j).

Пусть b[i][j] содержит количество путей, которыми осел может добраться из клетки (n, n) в клетку (i, j).

Количество способов, которыми Ходжа и осел могут встретиться в клетке (i, j), равно a[i][j] * b[i][j].

Для получения ответа остаётся вычислить сумму произведений по модулю 9929:

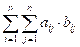mod 9929

Пример

Для n = 3 построим массивы:

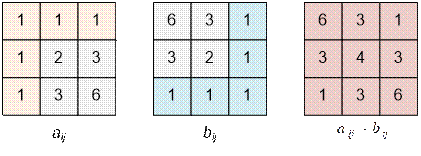
= (6 + 3 + 1) + (3 + 4 + 3) + (1 + 3 + 6) = 30

Реализация алгоритма

Объявим рабочие массивы.

#define MAX 55

#define MOD 9929

int a[MAX][MAX], b[MAX][MAX];

Читаем входное значение n.

scanf("%d", &n);

memset(a, 0, sizeof(a));

memset(b, 0, sizeof(b));

Вычисляем значения ячеек массивов a и b.

a[1][1] = 1;

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

a[i][j] = (a[i][j] + a[i - 1][j] + a[i][j - 1]) % MOD;

b[n][n] = 1;

for (i = n; i >= 1; i--)

for (j = n; j >= 1; j--)

b[i][j] = (b[i][j] + b[i + 1][j] + b[i][j + 1]) % MOD;

В переменной res находим количество способов, которыми Ходжа и осел могут встретиться.

res = 0;

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

res = (res + a[i][j] * b[i][j]) % MOD;

Выводим ответ.

printf("%d\n", res);