5101. Hodja Nasreddin

Hodja Nasreddin is located in the top-left cell of an n × n grid, while his donkey is in the bottom-right cell. Hodja can only move right or down, and the donkey can only move left or up.

How many ways can they meet in the same cell? Two ways are considered different if at least one of the routes of Hodja or the donkey is different from the other.

Input. One integer n (1 ≤ n ≤ 50).

Output. Print a single number – the number of ways in which Hodja and the donkey can meet. Since this number may be very large, print it modulo 9929.

Sample input	Sample output
3	30

SOLUTION

dynamic programming

Algorithm analysis

Let a[i][j] represent the number of ways in which Hodja Nasreddin can reach the cell (i, j) from (1, 1).

Let b[i][j] represent the number of ways in which donkey can reach the cell (i, j) from (n, n).

The number of ways in which Hodja and the donkey can meet at cell (i, j) is equal to a[i][j] * b[i][j].

To get the answer, it remains to compute the sum of products modulo 9929:

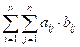mod 9929

Example

Let’s build the arrays for n = 3:

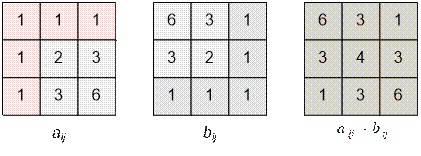
= (6 + 3 + 1) + (3 + 4 + 3) + (1 + 3 + 6) = 30

Algorithm realization

Declare the arrays.

#define MAX 55

#define MOD 9929

int a[MAX][MAX], b[MAX][MAX];

Read input value of n.

scanf("%d", &n);

memset(a, 0, sizeof(a));

memset(b, 0, sizeof(b));

Compute the values of the cells in arrays a and b.

a[1][1] = 1;

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

a[i][j] = (a[i][j] + a[i - 1][j] + a[i][j - 1]) % MOD;

b[n][n] = 1;

for (i = n; i >= 1; i--)

for (j = n; j >= 1; j--)

b[i][j] = (b[i][j] + b[i + 1][j] + b[i][j + 1]) % MOD;

In the variable res, find the number of ways in which Hodja and the donkey can meet.

res = 0;

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

res = (res + a[i][j] * b[i][j]) % MOD;

Print the answer.

printf("%d\n", res);