5103. Коза ностра
Пока у
школьников проходит зачёт, преподаватели играют в "Мафию". За круглым
столом сидят n преподавателей.
Ведущий должен раздать некоторым из них карты с тузами (тузов может быть любое
количество, включая 0) – эти преподаватели будут мафией. При этом никакие
два мафиози не должны сидеть рядом.
Сколькими
способами ведущий может раздать карты? Два способа считаются различными, если
существует хотя бы один преподаватель, который является мафией в одном случае и
не является мафией в другом.
Вход. Количество преподавателей n (1 ≤ n ≤ 30), сидящих по кругу.
Выход. Выведите одно число –
количество способов раздать карты.
|
Пример
входа 1 |
Пример
выхода 1 |
|
1 |
2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
2 |
3 |
РЕШЕНИЕ
числа
Фибоначчи
Анализ алгоритма
Пусть g(n) – количество способов раздать карты n преподавателям, выстроенным в ряд (первый и последний при этом не
считаются соседями). Эта задача эквивалентна подсчёту бинарных
последовательностей длины n,
состоящих из 0 и 1, в которых никакие две единицы не стоят рядом. Решением
является последовательность Фибоначчи, задаваемая следующей рекуррентной
формулой:
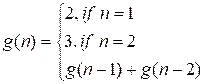
Пусть f(n) – количество способов раздать карты n преподавателям,
расположенным по кругу.
![]()
·
Если первому преподавателю туз не выдан, то
оставшимся n – 1 преподавателям тузы
можно раздать g(n – 1) способами.
·
Если же первому преподавателю выдан туз, то
второму и последнему преподавателям туз выдавать нельзя. Тогда оставшимся n – 3 преподавателям тузы можно раздать
g(n – 3) способами.
Таким
образом, получаем соотношение:
f(n) = g(n – 1) + g(n – 3), если n ≥ 3
Пример
При n = 3 нам потребуется значение g(0). Его можно найти из равенства g(0) + g(1) = g(2), откуда
g(0) = g(2) – g(1) = 3 – 2 = 1
Следовательно
f(3) = g(2) + g(0) = 3 + 1 = 4

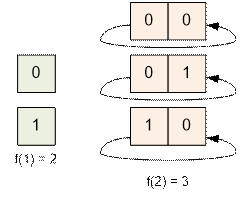
·
f(1) = 2
·
f(2) = 3
Реализация алгоритма
Объявим массив fib для хранения чисел Фибоначчи.
#define MAX 46
int fib[MAX];
Основная часть программы. Вычисляем числа Фибоначчи.
fib[0] = 1; fib[1] = 2;
for (int i = 2; i < MAX; i++)
fib[i] =
fib[i - 1] + fib[i - 2];
Читаем входное число n.
scanf("%d", &n);
Вычисляем ответ res.
if (n == 1) res = 2; else
if (n == 2) res = 3; else
res = fib[n - 1] + fib[n - 3];
Выводим ответ.
printf("%d\n", res);
Java реализация
import java.util.*;
public class Main
{
private static final int MAX = 46;
public static void main(String[] args)
{
Объявим массив fib для хранения чисел Фибоначчи.
int[] fib = new int[MAX];
Вычисляем числа Фибоначчи.
fib[0] = 1;
fib[1] = 2;
for (int i = 2; i < MAX; i++)
fib[i] = fib[i - 1] + fib[i - 2];
Читаем входное число n.
Scanner con = new Scanner(System.in);
int n = con.nextInt();
Вычисляем ответ res.
int res;
if (n == 1) res = 2;
else if (n == 2) res = 3;
else res = fib[n - 1] + fib[n - 3];
Выводим ответ.
System.out.println(res);
}
}
Python реализация
Объявим список fib для хранения чисел Фибоначчи.
fib
= [0] * 46
Вычисляем числа Фибоначчи.
fib[0] = 1
fib[1] = 2
for i in range(2, 46):
fib[i] = fib[i - 1] + fib[i - 2]
Читаем входное число n.
n = int(input())
Вычисляем ответ res.
if n == 1: res = 2
elif n == 2: res = 3
else: res = fib[n - 1] + fib[n - 3]
Выводим ответ.
print(res)