5103. Koza Nostra

While the students are taking an exam, the teachers are playing Mafia. There are n teachers sitting around a round table. The host must deal ace cards to some of them (the number of aces can be arbitrary, including 0) – these teachers will be the mafia. However, no two mafia members are allowed to sit next to each other.

In how many ways can the host deal the cards? Two ways are considered different if there exists at least one teacher who is a mafia member in one case and is not a mafia member in the other.

Input. The number of teachers n (1 ≤ n ≤ 30) sitting around the table.

Output. Print one integer – the number of ways to deal the cards.

Sample input 1	Sample output 1
1	2
Sample input 2	Sample output 2
2	3

SOLUTION

Fibonacci numbers

Algorithm analysis

Let g(n) be the number of ways to deal cards to n teachers arranged in a line (the first and the last are not considered adjacent). This problem is equivalent to counting binary sequences of length n consisting of 0s and 1s in which no two 1s are adjacent. The solution is given by the Fibonacci sequence defined by the following recurrence relation:

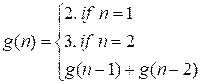
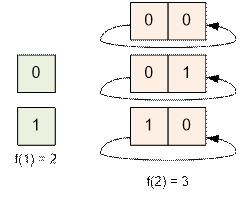
Let f(n) be the number of ways to deal cards to n teachers seated in a circle.

· If the first teacher does not receive an ace, then the remaining n − 1 teachers can be dealt aces in g(n − 1) ways.

· If the first teacher does receive an ace, then the second and the last teachers must not receive aces. In this case, the remaining n − 3 teachers can be dealt aces in g(n − 3) ways.

Thus, we obtain the following relation:

f(n) = g(n – 1) + g(n – 3), if n ≥ 3

Example

For n = 3, we need the value g(0). It can be found from the equality g(0) + g(1) = g(2), which gives

g(0) = g(2) – g(1) = 3 – 2 = 1

Therefore,

f(3) = g(2) + g(0) = 3 + 1 = 4

The base cases are as follows:

· f(1) = 2

· f(2) = 3

Algorithm implementation

Declare an array fib to store the Fibonacci numbers.

#define MAX 46

int fib[MAX];

The main part of the program. Compute the Fibonacci numbers.

fib[0] = 1; fib[1] = 2;

for (int i = 2; i < MAX; i++)

fib[i] = fib[i - 1] + fib[i - 2];

Read the input number n.

scanf("%d", &n);

Compute the answer res.

if (n == 1) res = 2; else

if (n == 2) res = 3; else

res = fib[n - 1] + fib[n - 3];

Print the answer.

printf("%d\n", res);

Java implementation

import java.util.*;

public class Main

{

private static final int MAX = 46;

public static void main(String[] args)

{

Declare an array fib to store the Fibonacci numbers.

int[] fib = new int[MAX];

Compute the Fibonacci numbers.

fib[0] = 1;

fib[1] = 2;

for (int i = 2; i < MAX; i++)

fib[i] = fib[i - 1] + fib[i - 2];

Read the input number n.

Scanner con = new Scanner(System.in);

int n = con.nextInt();

Compute the answer res.

int res;

if (n == 1) res = 2;

else if (n == 2) res = 3;

else res = fib[n - 1] + fib[n - 3];

Print the answer.

System.out.println(res);

}

}

Python implementation

Declare a list fib to store the Fibonacci numbers.

fib = [0] * 46

Compute the Fibonacci numbers.

fib[0] = 1

fib[1] = 2

for i in range(2, 46):

fib[i] = fib[i - 1] + fib[i - 2]

Read the input number n.

n = int(input())

Compute the answer res.

if n == 1: res = 2

elif n == 2: res = 3

else: res = fib[n - 1] + fib[n - 3]

Print the answer.

print(res)