5115. Хоккей на Урале

Для популяризации хоккея и повышения мастерства хоккейных команд Урала был организован Всеуральский турнир. Для участия в турнире были приглашены n хоккейных команд из городов Урала.

После первых двух туров, в каждом из которых каждая команда провела по одному матчу, оказалось, что команд слишком много. Организаторами турнира было решено допустить к дальнейшему участию только k команд, никакие две из которых не встречались в рамках первых двух туров.

Требуется написать программу, которая находит набор из k команд, удовлетворяющий условиям, либо выводит сообщение о том, что это сделать невозможно. В случае существования нескольких подходящих наборов необходимо найти любой из них.

Вход. В первой строке содержится число n (2 ≤ n ≤ 100000, n чётное). Следующие n строк содержат описания всех прошедших матчей. Описание каждого матча состоит из двух натуральных чисел, не превышающих n – номеров команд, игравших в матче. Первые n / 2 из них соответствуют матчам первого тура, оставшиеся – матчам второго тура. Последняя строка содержит одно число k (2 ≤ k ≤ n).

Гарантируется, что каждая команда сыграла ровно два матча: один в первом туре и один во втором.

Выход. Вывести либо единственное число 0, если решения не существует, либо k различных чисел – номера отобранных команд.

Пример входа 1	Пример выхода 1
6 1 2 3 5 4 6 2 3 4 5 1 6 3	1 4 3
Пример входа 2	Пример выхода 2
4 1 2 3 4 2 1 4 3 3	0

РЕШЕНИЕ

графы - циклы

Анализ алгоритма

Каждой хоккейной команде поставим в соответствие вершину графа. Сыгранные игры – ребра графа. Каждая команда провела в точности две игры. Степень каждой вершины графа равна 2, значит граф представляет собой набор простых циклов. В каждом цикле можно выбрать вершины (номера команд) через одну. Они нам подходят, так как они еще не играли между собой. Таким образом всегда можно выбрать не более n / 2 вершин. Следовательно решение существует только при k ≤ n / 2.

Пример

После сыгранных двух туров граф имеет вид одного цикла из 6 вершин.

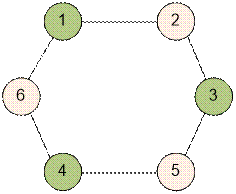
Отобранными могут быть команды, расположенные в цикле через один – например 1, 3, 4 или 2, 5, 6.

После двух туров, например, может сложиться следующая стуация:

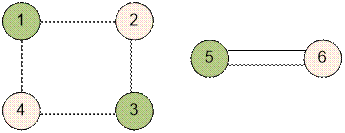
Граф представляет собой два цикла. Тогда отобранными могут быть команды 1, 3, 5 или 2, 4, 6.

Реализация алгоритма

Объявим список смежности графа g и рабочие массивы.

vector <vector <int> > g;

vector<int> used, res;

Поиск в глубину из вершины v. В массиве res запоминаем порядок обхода вершин.

void dfs(int v)

{

used[v] = 1;

res.push_back(v);

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (used[to] == 0) dfs(to);

}

}

Основная часть программы. Читаем входные данные. Строим граф.

scanf("%d", &n);

g.resize(n + 1);

for (i = 0; i < n; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

g[b].push_back(a);

}

scanf("%d", &k);

Граф может быть несвязным. Запускаем поиск в глубину на несвязном графе.

used.resize(n + 1);

for (i = 1; i <= n; i++)

if (used[i] == 0) dfs(i);

В зависимости от значения k выводим ответ. Решение существует только при k ≤ n / 2.

if (k <= n / 2)

{

for (i = 0; i < k; i++)

printf("%d ", res[2 * i]);

printf("\n");

}

else

puts("0");