5125. Подсчет курей

Куриный фермер Хиоян приобрел трех новых курей Люси, Чарли и ЦЦ. Хиоян хочет построить изгородь таким образом, чтобы каждая из них имела свой собственный беспрепятственный вид на округу. Изгородь должна иметь три стороны; это даст возможность каждой курице прогуливаться взад-вперед вдоль собственной стороны, не мешая другим. Хиоян нашел рулон проволочной сетки (ограждения) в сарае длиной в точности p футов. Она хочет вычислить количество способов, которыми сможет построить изгородь для курей таким образом, чтобы ее периметр был целочисленным, и при этом был бы использован весь рулон. Изгороди, полученные вращениями, считаются одинаковыми. Однако изгороди, полученные отражениями, могут быть разными (см. внизу).

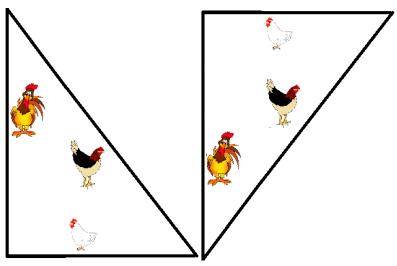
Одинаковые Разные

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 1000). Каждый тест следует обрабатывать независимо от других.

Каждый тест состоит из одной строки, содержащей номер теста и длину рулона сетки n (3 ≤ n ≤ 10000).

Выход. Для каждого теста вывести в одной строке номер теста и общее различное количество трехсторонних изгородей для курей, которые можно сделать при условии использования всего рулона.

Пример входа	Пример выхода
5 1 3 2 11 3 12 4 100 5 9999	1 l 2 5 3 4 4 392 5 4165834

РЕШЕНИЕ

геометрия - перебор

Анализ алгоритма

Пусть a ≤ b ≤ c – стороны треугольника (треугольной изгороди), a + b + c = p – периметр треугольника, равный длине найденного рулона проволочной сетки. Найдем границы самой длинной стороны c. Она будет наименьшей в случае разностороннего треугольника: c ≥ . И наибольшей, если сумма двух остальных сторон будет равна c + 1 при нечетном p, или c + 2 при четном p. В любом из этих случаев c < . Таким образом

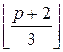≤ c < , что эквивалентно ≤ c ≤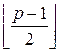

Перебираем значение с в указанном интервале, и подсчитываем для каждого из них количество искомых изгородей.

Каждый равносторонний или равнобедренный треугольник порождает один тип изгороди (треугольники, полученные их отражениями, будут такими же самыми). Треугольник с тремя различными сторонами порождает две разные изгороди (его отражения будут отличаться от исходного треугольника). Рассмотрим следующие случаи:

1. Если c = , то имеем один равносторонний треугольник.

2. Пусть (p – c) – четное число. Тогда обязательно существуют треугольники, у которых a = b и b = c, то есть две равнобедренные изгороди. Причем в случае a = b длина стороны a будет наибольшей и равной среди всех треугольников с фиксированными c и p (напомним, что значение с согласно выше приведенным ограничениям не может равняться половине периметра). А при b = c длина стороны a будет наименьшей и равной p – 2c. То есть

p – 2c ≤ a ≤ ,

причем при крайних значениях a получим равнобедренные треугольники. При остальных a все стороны треугольника будут разные. Обозначим L = p – 2c, R = . Тогда количество разных изгородей равно 2 (для двух равнобедренных треугольников) плюс 2 * (R – L – 1 ), если указанная разница положительна.

3. Пусть (p – c) – нечетное число. Тогда случая a = b быть не может. Значение a будет наибольшим при b = a + 1, и равно R = . Минимальным a будет при наибольшем b (случай b = c) и равно L = p – 2c. Таким образом

p – 2c ≤ a ≤

При a = p – 2c изгородь имеет вид равнобедренного треугольника. При остальных a стороны треугольника разные. Количество разных изгородей равно 1 (для одного равнобедренного треугольника) плюс 2 * (R – L), если указанная разница положительна.

Реализация алгоритма

Функция solve(p) возвращает количество искомых изгородей периметра p.

int solve(int p)

{

int c, cnt = 0;

for(c = (p - 1) / 2; c >= (p + 2) / 3; c--)

Случай, когда треугольник равносторонний.

if (c == p / 3) cnt++; else

Значение p – c четно. Возможны случаи a = b и b = c. В переменную L заносим наименьшее возможное значение а, в переменную R – наибольшее. Треугольники с разными сторонами будут получаться при a Î [L + 1; R – 1]. Всего таких треугольников будет

2 * (R – 1 – (L + 1) + 1) = 2 * (R – L – 1)

if ((p - c) % 2 == 0)

{

cnt += 2;

L = p - 2*c;

R = (p - c) / 2;

if (L + 1 <= R - 1) cnt += 2 * (R - L - 1);

}

Значение p – c нечетно. Для равнобедренного треугольника возможен только случай b = c, что достигается при наименьшем a. Треугольники с разными сторонами будут получаться при a Î [L + 1; R]. Всего таких треугольников будет

2 * (R – (L + 1) + 1) = 2 * (R – L)

else

{

L = p - 2*c;

R = (p - c - 1) / 2;

cnt++;

if (L + 1 <= R) cnt += 2 * (R - L);

}

return cnt;

}

Основная часть программы. Читаем входные данные. Вычисляем и выводим ответ.

scanf("%d",&tests);

for(i = 1; i <= tests; i++)

{

scanf("%d %d",&t,&n);

res = solve(n);

printf("%d %d\n",i, res);

}